Modelling of Running Performances: Comparisons of Power-Law, Hyperbolic, Logarithmic, and Exponential Models in Elite Endurance Runners

Abstract

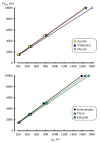
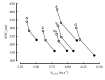
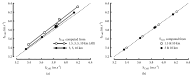
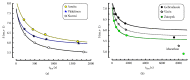
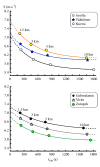
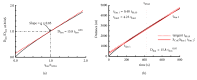
Many empirical and descriptive models have been proposed since the beginning of the 20^th century. In the present study, the power-law (Kennelly) and logarithmic (Péronnet-Thibault) models were compared with asymptotic models such as 2-parameter hyperbolic models (Hill and Scherrer), 3-parameter hyperbolic model (Morton), and exponential model (Hopkins). These empirical models were compared from the performance of 6 elite endurance runners (P. Nurmi, E. Zatopek, J. Väätäinen, L. Virén, S. Aouita, and H. Gebrselassie) who were world-record holders and/or Olympic winners and/or world or European champions. These elite runners were chosen because they participated several times in international competitions over a large range of distances (1500, 3000, 5000, and 10000 m) and three also participated in a marathon. The parameters of these models were compared and correlated. The less accurate models were the asymptotic 2-parameter hyperbolic models but the most accurate model was the asymptotic 3-parameter hyperbolic model proposed by Morton. The predictions of long-distance performances (maximal running speeds for 30 and 60 min and marathon) by extrapolation of the logarithmic and power-law models were more accurate than the predictions by extrapolation in all the asymptotic models. The overestimations of these long-distance performances by Morton's model were less important than the overestimations by the other asymptotic models.

Figure 1

(a) Individual linear relationships (power-law model) with logarithmic scales for running speed and t_lim. The performances by Nurmi and Zatopek were the same for the 1500 m distance. (b) Extrapolation of the linear relationships (dashed lines) to marathon performances.

Figure 2

Linear relationships between exhaustion time (t_lim) and distance (D_lim).

Figure 3

Relation between critical speed and Anaerobic Distance Capacity (ADC₁) for different ranges of distances: 1500 to 5000 m (black dots), 3000 to 10000 m (empty circles), and 1500 to 10000 m (grey dots).

Figure 4

(a) Individual S-1/t_lim relationships in elite endurance runners. ((b) and (c)) Individual hyperbolic curves corresponding to S_Crit1 model (dashed curves) and S_Crit2 model (solid curves).

Figure 5

(a) Relationships between the individual values of S_Crit1 and S_Crit2 computed from 3 distances (black dots) or 4 distances (empty circles). (b) Relationships between S_Crit1 and S_Crit2 computed from 2 distances, only.

Figure 6

Relationship between running speed (S) and time (t_lim) in Morton's model computed from 1500 to 10000 m. (b) The same model in the three subjects who ran the marathon.

Figure 7

(a) Individual linear regressions between the logarithms of t_lim and running speeds. The data corresponding to 1.5 km were not included in the computation of the regressions. The performances by Nurmi and Zatopek were the same for the 1500 m distance. (b) Extrapolation of the speed-ln(t_lim) relationships of the 3000-10000 m performances to t_lim corresponding to a marathon (dashed lines). The scale of t_lim is a logarithmic scale.

Figure 8

Individual relationships between running speed and t_lim in the Hopkins model computed with 4 distances (1500-10000 m).

Figure 9

Comparisons of the relationship between (t_lim) and running speed (S) of the logarithmic model, power-law model, S_Crit1 and S_Crit2 models, Morton's model, and exponential model computed from 4 distance performances (1500, 3000, 5000, and 10000 m; empty circles) in the three runners who participated in marathon (black dots).

Figure 10

Relation between S_Crit1 and ADC₁ in the 19 elite runners whose ranges of performances were different: 1500-10000 m (black dots), 5000-10000 m (empty circles), and 3000-5000 m (grey dots).

Figure 11

Effect of t_MAS (T) on the ratio E_T/E_7min for an elite endurance runner (E_7min = 4), a medium level endurance runner (E_7min = 8), and a low-level endurance runner (E_7min = 16).

Figure 12

(a) Slope of the tangent at t_MAS of the curve corresponding to the power-law model with t_lim normalised to t_MAS and D_lim normalised to D_lim at maximal aerobic speed (MAS). (b) Comparison of a critical speed computed from two values of t_lim with the tangent at t_MAS (420s).

Figure 13

Individual relationships between speed and t_lim computed from the mean values of ADC and S_Crit in (12) and (14).