Analytical solution for converging elliptic shear wave in a bounded transverse isotropic viscoelastic material with nonhomogeneous outer boundary

Abstract

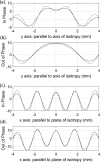
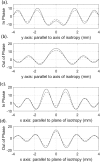
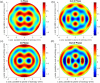
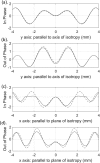
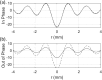
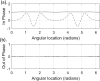
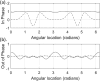
Dynamic elastography methods-based on optical, ultrasonic, or magnetic resonance imaging-are being developed for quantitatively mapping the shear viscoelastic properties of biological tissues, which are often altered by disease and injury. These diagnostic imaging methods involve analysis of shear wave motion in order to estimate or reconstruct the tissue's shear viscoelastic properties. Most reconstruction methods to date have assumed isotropic tissue properties. However, application to tissues like skeletal muscle and brain white matter with aligned fibrous structure resulting in local transverse isotropic mechanical properties would benefit from analysis that takes into consideration anisotropy. A theoretical approach is developed for the elliptic shear wave pattern observed in transverse isotropic materials subjected to axisymmetric excitation creating radially converging shear waves normal to the fiber axis. This approach, utilizing Mathieu functions, is enabled via a transformation to an elliptic coordinate system with isotropic properties and a ratio of minor and major axes matching the ratio of shear wavelengths perpendicular and parallel to the plane of isotropy in the transverse isotropic material. The approach is validated via numerical finite element analysis case studies. This strategy of coordinate transformation to equivalent isotropic systems could aid in analysis of other anisotropic tissue structures.

FIG. 1.

(Color online) Transversely isotropic cylindrical sample with x–z plane of isotropy (fibers in the y direction) subjected to a nonhomogeneous boundary condition: harmonic displacement in the z direction of amplitude $u_{z{r}_0}$ at frequency $f=\omega /2\pi$ on its curved boundary at $r=r_0$: (a) a three-dimensional rendering with the $x,y$ “viewing plane” indicated, which is the plane used for Figs. 2 and 5; (b) viewed in $x,y$ plane, which is a plane of symmetry; fibers shown along the y axis, the axis of isotropy; (c) viewed in $x,y\prime$ plane after transformation to an elliptic coordinate system $\{\xi ,\eta \}$ with isotropic material properties.

FIG. 2.

(Color online) Normalized z direction displacement $(u_{\mathit{z}\mathit{r}}/u_{z{r}_0})$ on the x–y plane for the case $\varphi =1$ and $\eta =0.01$ using the theoretical model [(a) in phase, (b) 90 degrees out of phase] and the FE model [(c) in phase, (d) 90 degrees out of phase]. See supplementary material (Ref. 57).

FIG. 3.

Normalized z direction displacement $(u_{\mathit{z}\mathit{r}}/u_{z{r}_0})$ for the case $\varphi =1.0$ and $\eta =0.01$ using the theoretical model (solid line) and the FE model (dashed line): (a) along the y (fiber) axis in phase: ${\Delta }_y=26\%$; (b) along the y (fiber) axis 90 degrees out of phase: ${\Delta }_y=16\%$; (c) along the x axis in phase: ${\Delta }_x=28\%$ (d) along the x axis 90 degrees out of phase: ${\Delta }_x=12\%$.

FIG. 4.

Normalized z direction displacement $(u_{\mathit{z}\mathit{r}}/u_{z{r}_0})$ for the case $\varphi =0.1$ and $\eta =0.01$ using the theoretical model (solid line) and the FE model (dashed line): (a) along the y (fiber) axis in phase: ${\Delta }_y=22\%$; (b) along the y (fiber) axis 90 degrees out of phase: ${\Delta }_y=17\%$; (c) along the x axis in phase: ${\Delta }_x=16\%$; (d) along the x axis 90 degrees out of phase: ${\Delta }_y=15\%$.

FIG. 5.

(Color online) Normalized z direction displacement $(u_{\mathit{z}\mathit{r}}/u_{z{r}_0})$ on the x–y plane for the case $\varphi =1$ and $\eta =0.15$ using the theoretical model [(a) in phase, (b) 90 degrees out of phase] and the FE model [(c) in phase, (d) 90 degrees out of phase]. See supplementary material (Ref. 57).

FIG. 6.

Normalized z direction displacement $(u_{\mathit{z}\mathit{r}}/u_{z{r}_0})$ for the case $\varphi =1.0$ and $\eta =0.15$ using the theoretical model (solid line) and the FE model (dashed line): (a) along the y (fiber) axis in phase: ${\Delta }_y=6.0\%$; (b) along the y (fiber) axis 90 degrees out of phase: ${\Delta }_y=9.6\%$; (c) along the x axis in phase: ${\Delta }_x=41\%$; (d) along the x axis 90 degrees out of phase: ${\Delta }_x=31\%$.

FIG. 7.

Normalized z direction displacement $(u_{\mathit{z}\mathit{r}}/u_{z{r}_0})$ for the case $\varphi =0.1$ and $\eta =0.15$ using the theoretical model (solid line) and the FE model (dashed line): (a) along the y (fiber) axis in phase: ${\Delta }_y=6.3\%$; (b) along the y (fiber) axis 90 degrees out of phase: ${\Delta }_y=2.5\%$; (c) along the x axis in phase: ${\Delta }_x=29\%$; (d) along the x axis 90 degrees out of phase: ${\Delta }_x=7.4\%$.

FIG. 8.

Normalized z direction displacement $(u_{\mathit{z}\mathit{r}}/u_{z{r}_0})$ for the case $\varphi =0$ and $\eta =0.01$ using the theoretical model (solid line) and the FE model (dashed line): (a) along a diameter in phase: ${\Delta }_r=3.54\%$; (b) along a diameter 90 degrees out of phase: ${\Delta }_r=109\%$.

FIG. 9.

Normalized z direction displacement $(u_{\mathit{z}\mathit{r}}/u_{z{r}_0})$ for the case $\varphi =0$ and $\eta =0.15$ using the theoretical model (solid line) and the FE model (dashed line): (a) along a diameter in phase: ${\Delta }_r=1.74\%$; (b) along a diameter 90 degrees out of phase: ${\Delta }_r=0.8\%$. (Dashed line difficult to see because of close match).

FIG. 10.

Normalized z direction displacement $(u_{\mathit{z}\mathit{r}}/u_{z{r}_0})$ on the outer boundary of the cylinder at $r=r_0$ for $\theta$ from $0\hspace{0.17em}\hspace{0.17em}\text{to}\hspace{0.17em}2\pi$ radians for the case $\varphi =1$ and $\eta =0.01$ using the theoretical model [(a) in phase, (b) 90 degrees out of phase]. The solid line is the solution of the summation in Eq. (9) using n = 0,…, 9. The dashed line is the first term only (n = 0).

FIG. 11.

Normalized z direction displacement $(u_{\mathit{z}\mathit{r}}/u_{z{r}_0})$ on the outer boundary of the cylinder at $r=r_0$ for $\theta$ from $0\hspace{0.17em}\text{to}\hspace{0.17em}2\pi$ radians for the case $\varphi =1$ and $\eta =0.15$ using the theoretical model [(a) in phase, (b) 90 degrees out of phase]. The solid line is the solution of the summation in Eq. (9) using n = 0,…, 9. The dashed line is the first term only (n = 0).