Dissipative shock waves generated by a quantum-mechanical piston

Abstract

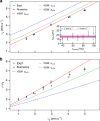
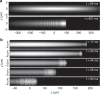
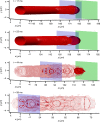
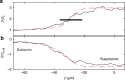
The piston shock problem is a prototypical example of strongly nonlinear fluid flow that enables the experimental exploration of fluid dynamics in extreme regimes. Here we investigate this problem for a nominally dissipationless, superfluid Bose-Einstein condensate and observe rich dynamics including the formation of a plateau region, a non-expanding shock front, and rarefaction waves. Many aspects of the observed dynamics follow predictions of classical dissipative-rather than superfluid dispersive-shock theory. The emergence of dissipative-like dynamics is attributed to the decay of large amplitude excitations at the shock front into turbulent vortex excitations, which allow us to invoke an eddy viscosity hypothesis. Our experimental observations are accompanied by numerical simulations of the mean-field, Gross-Pitaevskii equation that exhibit quantitative agreement with no fitting parameters. This work provides an avenue for the investigation of quantum shock waves and turbulence in channel geometries, which are currently the focus of intense research efforts.

Fig. 1

Experimental set-up and integrated cross sections. a A repulsive barrier (piston) is swept from right to left through a BEC with speed v_p. A bulge forms at the interface of the BEC and the piston. Image is not to scale. b Experimental images and corresponding integrated cross sections for experiment (green) and numerics (blue) at times t = 0, 60, 100, and 140 ms into a v_p = 2 mm s⁻¹ sweep

Fig. 2

Shock speed, peak density, and shock width vs. piston speed. Analyzed experimental (green dots) and numerical (blue triangles) results for increasing piston velocity are plotted with overlaid theory curves for VSW (red solid line), using an effective c_s,eff = 1.35 mm s⁻¹ obtained from a fit of the experimental and numerical data to the VSW theory prediction. VSW theory curves are also calculated for c_s,1d = 1.75 mm s⁻¹ (green dashed) and c_s,bulk = 2.47 mm s⁻¹ (blue dot-dashed). a Shock front speed. Inset, Shock front width at different times for piston speeds 2 mm s⁻¹ (blue solid) and 3 mm s⁻¹ (red dashed), with corresponding error (shaded regions). b The normalized plateau density is determined by measuring the plateau integrated density when the piston reaches the center of the BEC. Weighted mean ± s.d. are plotted for three (a) and five (b) sets of data. For more information, see text

Fig. 3

Integrated cross sections of numerical simulations. a Quasi-1D dispersive shock wave in low atom number regime where v_p = 0.41 mm s⁻¹. b Development of 3D turbulence and a viscous shock wave in the large atom number regime where v_p = 2.44 mm s⁻¹

Fig. 4

Isosurfaces of 3D numerical simulation. A piston front (rightmost, non-transparent green plane) sweeping into an elongated BEC at v_p = 2.44 mm s⁻¹. The shock front (leftmost, blue transparent plane) propagates through the BEC over time. At time t = 58 ms, only the shock front plane is shown. In the plateau region between the two planes, vortex tangles are generated. The isosurface density value is 0.1 ⋅ Γ, semi-transparent for $\sqrt{x^2+y^2}>2.39\mu \mathrm{m}$ to visualize the BEC interior

Fig. 5

Experimental evidence of vortex turbulence. The barrier is swept to the center of the BEC in 87 ms (v_p = 2.5 mm s⁻¹). Within the plateau region, a vortex rings, b soliton y-forks, and c soliton snaking are observed. Absorption images are taken after 10.1 ms of free expansion. Black dashed lines are intended as a guide to the eye

Fig. 6

Shock profile. a Filtered density and b velocity profiles from 3D numerical simulation (black solid) in units of the downstream, subsonic flow density ${\overline{\rho }}_0$ and associated sound speed c_s,eff = 1.35 mm s⁻¹. The red dashed curves correspond to an exact, viscous traveling wave solution of the piston problem for the 1D shallow water equations with an effective nondimensional viscosity parameter (see Methods) that reveals the shock structure and compares favorably to the experimentally measured shock width 15.5 μm (horizontal segment). This profile corresponds to Fig. 3 at the time t = 83 ms

Fig. 7

Rarefaction waves. A BEC initially confined to the left half of the trap is suddenly allowed to spread to the right. The plot shows the edge position vs. time, where experiment (green dots) and numerics (blue triangles) are plotted overlaid with expected results for 2c_s,bulk (orange dashed) and 2c_s,1d (red dot-dashed). Experimental data are mean ± s.d. for five runs at each measured time, where the green and blue solid lines are best fits to experiment and numerics, respectively. See text for more information