pKa measurements for the SAMPL6 prediction challenge for a set of kinase inhibitor-like fragments
- PMID: 30406372
- PMCID: PMC6367941
- DOI: 10.1007/s10822-018-0168-0
pKa measurements for the SAMPL6 prediction challenge for a set of kinase inhibitor-like fragments
Abstract
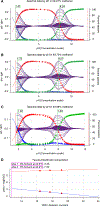
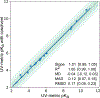
Determining the net charge and protonation states populated by a small molecule in an environment of interest or the cost of altering those protonation states upon transfer to another environment is a prerequisite for predicting its physicochemical and pharmaceutical properties. The environment of interest can be aqueous, an organic solvent, a protein binding site, or a lipid bilayer. Predicting the protonation state of a small molecule is essential to predicting its interactions with biological macromolecules using computational models. Incorrectly modeling the dominant protonation state, shifts in dominant protonation state, or the population of significant mixtures of protonation states can lead to large modeling errors that degrade the accuracy of physical modeling. Low accuracy hinders the use of physical modeling approaches for molecular design. For small molecules, the acid dissociation constant (pKa) is the primary quantity needed to determine the ionic states populated by a molecule in an aqueous solution at a given pH. As a part of SAMPL6 community challenge, we organized a blind pKa prediction component to assess the accuracy with which contemporary pKa prediction methods can predict this quantity, with the ultimate aim of assessing the expected impact on modeling errors this would induce. While a multitude of approaches for predicting pKa values currently exist, predicting the pKas of drug-like molecules can be difficult due to challenging properties such as multiple titratable sites, heterocycles, and tautomerization. For this challenge, we focused on set of 24 small molecules selected to resemble selective kinase inhibitors-an important class of therapeutics replete with titratable moieties. Using a Sirius T3 instrument that performs automated acid-base titrations, we used UV absorbance-based pKa measurements to construct a high-quality experimental reference dataset of macroscopic pKas for the evaluation of computational pKa prediction methodologies that was utilized in the SAMPL6 pKa challenge. For several compounds in which the microscopic protonation states associated with macroscopic pKas were ambiguous, we performed follow-up NMR experiments to disambiguate the microstates involved in the transition. This dataset provides a useful standard benchmark dataset for the evaluation of pKa prediction methodologies on kinase inhibitor-like compounds.
Keywords: Acid dissociation constants; Blind prediction challenge; Macroscopic pK a; Macroscopic protonation state; Microscopic pK a; Microscopic protonation state; SAMPL; Spectrophotometric pK a measurement.
Figures






Similar articles
-
Overview of the SAMPL6 pKa challenge: evaluating small molecule microscopic and macroscopic pKa predictions.J Comput Aided Mol Des. 2021 Feb;35(2):131-166. doi: 10.1007/s10822-020-00362-6. Epub 2021 Jan 4. J Comput Aided Mol Des. 2021. PMID: 33394238 Free PMC article.
-
SAMPL6: calculation of macroscopic pKa values from ab initio quantum mechanical free energies.J Comput Aided Mol Des. 2018 Oct;32(10):1203-1216. doi: 10.1007/s10822-018-0138-6. Epub 2018 Aug 6. J Comput Aided Mol Des. 2018. PMID: 30084080 Free PMC article.
-
High accuracy quantum-chemistry-based calculation and blind prediction of macroscopic pKa values in the context of the SAMPL6 challenge.J Comput Aided Mol Des. 2018 Oct;32(10):1139-1149. doi: 10.1007/s10822-018-0145-7. Epub 2018 Aug 23. J Comput Aided Mol Des. 2018. PMID: 30141103
-
Overview of the SAMPL5 host-guest challenge: Are we doing better?J Comput Aided Mol Des. 2017 Jan;31(1):1-19. doi: 10.1007/s10822-016-9974-4. Epub 2016 Sep 22. J Comput Aided Mol Des. 2017. PMID: 27658802 Free PMC article. Review.
-
Computation of pH-dependent binding free energies.Biopolymers. 2016 Jan;105(1):43-9. doi: 10.1002/bip.22702. Biopolymers. 2016. PMID: 26202905 Free PMC article. Review.
Cited by
-
Enhancing Carbon Acid pKa Prediction by Augmentation of Sparse Experimental Datasets with Accurate AIBL (QM) Derived Values.Molecules. 2021 Feb 17;26(4):1048. doi: 10.3390/molecules26041048. Molecules. 2021. PMID: 33671348 Free PMC article.
-
COSMO-RS based predictions for the SAMPL6 logP challenge.J Comput Aided Mol Des. 2020 Apr;34(4):385-392. doi: 10.1007/s10822-019-00259-z. Epub 2019 Nov 26. J Comput Aided Mol Des. 2020. PMID: 31773462
-
SAMPL7: Host-guest binding prediction by molecular dynamics and quantum mechanics.J Comput Aided Mol Des. 2021 Jan;35(1):63-77. doi: 10.1007/s10822-020-00357-3. Epub 2020 Nov 5. J Comput Aided Mol Des. 2021. PMID: 33150463
-
SAMPL6 challenge results from predictions based on a general Gaussian process model.J Comput Aided Mol Des. 2018 Oct;32(10):1165-1177. doi: 10.1007/s10822-018-0169-z. Epub 2018 Oct 15. J Comput Aided Mol Des. 2018. PMID: 30324305 Free PMC article.
-
Thermodynamics of Pillararene•Guest Complexation: Blinded Dataset for the SAMPL9 Challenge.New J Chem. 2022 Jan 21;46(3):995-1002. doi: 10.1039/d1nj05209h. Epub 2021 Dec 13. New J Chem. 2022. PMID: 35250257 Free PMC article.
References
-
- Mobley DL, Chodera JD, Isaacs L, Gibb BC. Advancing predictive modeling through focused development of model systems to drive new modeling innovations. UC Irvine: Department of Pharmaceutical Sciences, UCI; 2016; https://escholarship.org/uc/item/7cf8c6cr.
-
- Drug Design Data Resource, SAMPL;. https://drugdesigndata.org/about/sampl.
-
- Guthrie JP. A Blind Challenge for Computational Solvation Free Energies: Introduction and Overview. J Phys Chem B. 2009. January; 113(14):4501–4507. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Research Materials

