Microvscular networks with uniform flow
- PMID: 30420333
- PMCID: PMC6599712
- DOI: 10.1016/j.jtbi.2018.10.049
Microvscular networks with uniform flow
Abstract
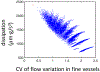
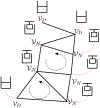
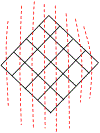
Within animals, oxygen exchange occurs within vascular transport networks containing potentially billions of microvessels that are distributed throughout the body. By comparison, large blood vessels are theorized to minimize transport costs, leading to tree-like networks that satisfy Murray's law. We know very little about the principles underlying the organization of healthy micro-vascular networks. Indeed capillary networks must also perfuse tissues with oxygen, and efficient perfusion may be incompatible with minimization of transport costs. While networks that minimize transport costs have been well-studied, other optimization principles have received much less scrutiny. In this work we derive the morphology of networks that uniformize blood flow distribution, inspired by the zebrafish trunk micro-vascular network. To find uniform flow networks, we devise a gradient descent algorithm able to optimize arbitrary differentiable objective functions on transport networks, while exactly respecting arbitrary differentiable constraint functions. We prove that in a class of networks that we call stackable, which includes a model capillary bed, the uniform flow network will have the same flow as a uniform conductance network, i.e., in which all edges have the same conductance. This result agrees with uniform flow capillary bed network found by the algorithm. We also show that the uniform flow completely explains the observed radii within the zebrafish trunk vasculature. In addition to deriving new results on optimization of uniform flow in micro-vascular networks, our algorithm provides a general method for testing hypotheses about possible optimization principles underlying real microvascular networks, including exposing tradeoffs between flow uniformity and transport cost.
Keywords: Blood flow; Capillary; Constrained optimization; Gradient descent; Phase transition; Zebrafish.
Copyright © 2018 Elsevier Ltd. All rights reserved.
Figures



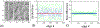



References
-
- Acheson David J. Elementary fluid dynamics. Oxford University Press, 1990.
-
- Ayata Cenk, Andrew K Dunn Yasemin Gursoy-Özdemir, Huang Zhihong, Boas David A, and Moskowitz Michael A. Laser speckle flowmetry for the study of cerebrovascular physiology in normal and ischemic mouse cortex. Journal of Cerebral Blood Flow & Metabolism, 24(7):744–755, 2004. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Miscellaneous

