Comparing Bayesian and non-Bayesian accounts of human confidence reports
- PMID: 30422974
- PMCID: PMC6258566
- DOI: 10.1371/journal.pcbi.1006572
Comparing Bayesian and non-Bayesian accounts of human confidence reports
Abstract
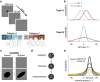
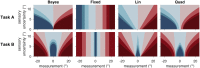
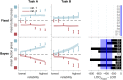
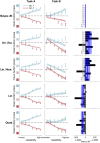
Humans can meaningfully report their confidence in a perceptual or cognitive decision. It is widely believed that these reports reflect the Bayesian probability that the decision is correct, but this hypothesis has not been rigorously tested against non-Bayesian alternatives. We use two perceptual categorization tasks in which Bayesian confidence reporting requires subjects to take sensory uncertainty into account in a specific way. We find that subjects do take sensory uncertainty into account when reporting confidence, suggesting that brain areas involved in reporting confidence can access low-level representations of sensory uncertainty, a prerequisite of Bayesian inference. However, behavior is not fully consistent with the Bayesian hypothesis and is better described by simple heuristic models that use uncertainty in a non-Bayesian way. Both conclusions are robust to changes in the uncertainty manipulation, task, response modality, model comparison metric, and additional flexibility in the Bayesian model. Our results suggest that adhering to a rational account of confidence behavior may require incorporating implementational constraints.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures

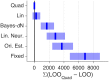
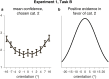
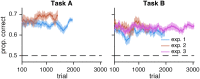
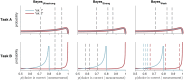


References
-
- Meyniel F, Sigman M, Mainen ZF. Confidence as Bayesian probability: From neural origins to behavior. Neuron. 2015. October;88(1):78–92. 10.1016/j.neuron.2015.09.039 - DOI - PubMed
-
- Brown AS. A review of the tip-of-the-tongue experience. Psychol Bull. 1991. March;109(2):204–223. 10.1037/0033-2909.109.2.204 - DOI - PubMed
-
- Persaud N, McLeod P, Cowey A. Post-decision wagering objectively measures awareness. Nat Neurosci. 2007. January;10(2):257–261. 10.1038/nn1840 - DOI - PubMed
-
- Bahrami B, Olsen K, Latham PE, Roepstorff A. Optimally interacting minds. Science. 2010;329(5995):1081–1085. 10.1126/science.1185718 - DOI - PMC - PubMed
-
- Fleming SM, Weil RS, Nagy Z, Dolan RJ, Rees G. Relating introspective accuracy to individual differences in brain structure. Science. 2010. September;329(5998):1541–1543. 10.1126/science.1191883 - DOI - PMC - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

