Semantic information, autonomous agency and non-equilibrium statistical physics
- PMID: 30443338
- PMCID: PMC6227811
- DOI: 10.1098/rsfs.2018.0041
Semantic information, autonomous agency and non-equilibrium statistical physics
Abstract
Shannon information theory provides various measures of so-called syntactic information, which reflect the amount of statistical correlation between systems. By contrast, the concept of 'semantic information' refers to those correlations which carry significance or 'meaning' for a given system. Semantic information plays an important role in many fields, including biology, cognitive science and philosophy, and there has been a long-standing interest in formulating a broadly applicable and formal theory of semantic information. In this paper, we introduce such a theory. We define semantic information as the syntactic information that a physical system has about its environment which is causally necessary for the system to maintain its own existence. 'Causal necessity' is defined in terms of counter-factual interventions which scramble correlations between the system and its environment, while 'maintaining existence' is defined in terms of the system's ability to keep itself in a low entropy state. We also use recent results in non-equilibrium statistical physics to analyse semantic information from a thermodynamic point of view. Our framework is grounded in the intrinsic dynamics of a system coupled to an environment, and is applicable to any physical system, living or otherwise. It leads to formal definitions of several concepts that have been intuitively understood to be related to semantic information, including 'value of information', 'semantic content' and 'agency'.
Keywords: agency; autonomy; entropy; information theory; non-equilibrium; semantic information.
Conflict of interest statement
We declare we have no competing interests.
Figures
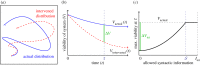
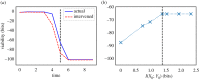
 , is the minimum level of syntactic information at which no viability is lost. Itot is the total amount of syntactic information between system and environment. (Online version in colour.)
, is the minimum level of syntactic information at which no viability is lost. Itot is the total amount of syntactic information between system and environment. (Online version in colour.)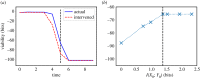

Similar articles
-
A theory of pragmatic information and its application to the quasi-species model of biological evolution.Biosystems. 2002 Aug-Sep;66(3):105-19. doi: 10.1016/s0303-2647(02)00038-2. Biosystems. 2002. PMID: 12413744
-
The Natural Philosophy of Economic Information: Autonomous Agents and Physiosemiosis.Entropy (Basel). 2021 Feb 25;23(3):277. doi: 10.3390/e23030277. Entropy (Basel). 2021. PMID: 33669029 Free PMC article.
-
Two Forms of Functional Reductionism in Physics.Synthese. 2024;203(2):66. doi: 10.1007/s11229-024-04507-0. Epub 2024 Feb 15. Synthese. 2024. PMID: 40226539 Free PMC article.
-
A Semantic Generalization of Shannon's Information Theory and Applications.Entropy (Basel). 2025 Apr 24;27(5):461. doi: 10.3390/e27050461. Entropy (Basel). 2025. PMID: 40422416 Free PMC article. Review.
-
The application of thermodynamic principles to histochemical and morphometric tissue research: principles and practical outline with focus on the glycosciences.Cell Tissue Res. 1999 Jun;296(3):443-55. doi: 10.1007/s004410051305. Cell Tissue Res. 1999. PMID: 10370131 Review.
Cited by
-
The Grayness of the Origin of Life.Life (Basel). 2021 May 29;11(6):498. doi: 10.3390/life11060498. Life (Basel). 2021. PMID: 34072344 Free PMC article.
-
Subjective Information and Survival in a Simulated Biological System.Entropy (Basel). 2022 May 2;24(5):639. doi: 10.3390/e24050639. Entropy (Basel). 2022. PMID: 35626524 Free PMC article.
-
Exploring Information and Communication Theories for Synthetic Cell Research.Front Bioeng Biotechnol. 2022 Jul 14;10:927156. doi: 10.3389/fbioe.2022.927156. eCollection 2022. Front Bioeng Biotechnol. 2022. PMID: 35910013 Free PMC article. No abstract available.
-
Psychophysical identity and free energy.J R Soc Interface. 2020 Aug;17(169):20200370. doi: 10.1098/rsif.2020.0370. Epub 2020 Aug 5. J R Soc Interface. 2020. PMID: 32752995 Free PMC article.
-
What does it mean to be an agent?Front Psychol. 2023 Oct 17;14:1273470. doi: 10.3389/fpsyg.2023.1273470. eCollection 2023. Front Psychol. 2023. PMID: 37915525 Free PMC article.
References
-
- Dretske F. 1981. Knowledge and the flow of information. Cambridge, MA: MIT Press.
-
- Shea N. 2007. Representation in the genome and in other inheritance systems. Biol. Phil. 22, 313–331. (10.1007/s10539-006-9046-6) - DOI
-
- Godfrey-Smith P, Sterelny K. 2016. Biological information. In The Stanford encyclopedia of philosophy (ed. Zalta EN.), summer 2016 edn. Metaphysics Research Lab, Stanford University.
-
- Godfrey-Smith P. 2007. Information in biology. In The Cambridge companion to the philosophy of biology (eds D Hull, M Ruse). Cambridge Companions to Philosophy, pp. 103–119. Cambridge, UK: Cambridge University Press. (10.1017/CCOL9780521851282.006) - DOI
-
- Collier J. 2008. Information in biological systems. In Handbook of philosophy of science. Volume 8: Philosophy of information, pp. 763–787. Amsterdam, The Netherlands, Elsevier.
LinkOut - more resources
Full Text Sources

