Whole-Brain Neuronal Activity Displays Crackling Noise Dynamics
- PMID: 30449656
- PMCID: PMC6307982
- DOI: 10.1016/j.neuron.2018.10.045
Whole-Brain Neuronal Activity Displays Crackling Noise Dynamics
Abstract
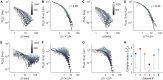
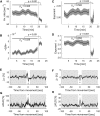
Previous studies suggest that the brain operates at a critical point in which phases of order and disorder coexist, producing emergent patterned dynamics at all scales and optimizing several brain functions. Here, we combined light-sheet microscopy with GCaMP zebrafish larvae to study whole-brain dynamics in vivo at near single-cell resolution. We show that spontaneous activity propagates in the brain's three-dimensional space, generating scale-invariant neuronal avalanches with time courses and recurrence times that exhibit statistical self-similarity at different magnitude, temporal, and frequency scales. This suggests that the nervous system operates close to a non-equilibrium phase transition, where a large repertoire of spatial, temporal, and interactive modes can be supported. Finally, we show that gap junctions contribute to the maintenance of criticality and that, during interactions with the environment (sensory inputs and self-generated behaviors), the system is transiently displaced to a more ordered regime, conceivably to limit the potential sensory representations and motor outcomes.
Keywords: GcaMP; calcium imaging; gap junctions; light-sheet microscopy; motor behavior; phase transitions; scale invariance; sensory modulation; whole-brain dynamics; zebrafish.
Copyright © 2018 The Author(s). Published by Elsevier Inc. All rights reserved.
Figures






Comment in
-
Cracklin' Fish Brains.Epilepsy Curr. 2019 Mar-Apr;19(2):112-114. doi: 10.1177/1535759719835348. Epilepsy Curr. 2019. PMID: 30955431 Free PMC article.
References
-
- Ahrens M.B., Orger M.B., Robson D.N., Li J.M., Keller P.J. Whole-brain functional imaging at cellular resolution using light-sheet microscopy. Nat. Methods. 2013;10:413–420. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Medical
Molecular Biology Databases
Miscellaneous

