Measurability of the epidemic reproduction number in data-driven contact networks

Abstract

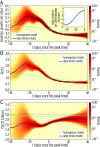
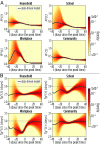
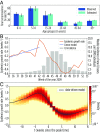
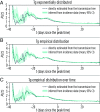
The basic reproduction number is one of the conceptual cornerstones of mathematical epidemiology. Its classical definition as the number of secondary cases generated by a typical infected individual in a fully susceptible population finds a clear analytical expression in homogeneous and stratified mixing models. Along with the generation time (the interval between primary and secondary cases), the reproduction number allows for the characterization of the dynamics of an epidemic. A clear-cut theoretical picture, however, is hardly found in real data. Here, we infer from highly detailed sociodemographic data two multiplex contact networks representative of a subset of the Italian and Dutch populations. We then simulate an infection transmission process on these networks accounting for the natural history of influenza and calibrated on empirical epidemiological data. We explicitly measure the reproduction number and generation time, recording all individual-level transmission events. We find that the classical concept of the basic reproduction number is untenable in realistic populations, and it does not provide any conceptual understanding of the epidemic evolution. This departure from the classical theoretical picture is not due to behavioral changes and other exogenous epidemiological determinants. Rather, it can be simply explained by the (clustered) contact structure of the population. Finally, we provide evidence that methodologies aimed at estimating the instantaneous reproduction number can operationally be used to characterize the correct epidemic dynamics from incidence data.

Keywords: computational modeling; generation time; infectious diseases; multiplex networks; reproduction number.

Fig. 1.

Model structure. (A) Visualization of the multiplex network representing a subsample of 10,000 individuals of the synthetic population. Note that the community layer is a complete graph, although not all edges are visible for the sake of readability of the illustration. (B) Degree distributions in the school, household, and workplace layers. (C) Schematic representation of the infection transmission model along with examples of the computation of individual reproduction number and generation time for the simulated transmission chains. I, infectious; R, removed; S, susceptible.

Fig. 2.

Fundamental epidemiological indicators. (A) Mean daily exponential epidemic growth rate, $r$, over time of the data-driven and homogeneous models. The colored area shows the density distribution of $r\left(t\right)$ values obtained in the single realizations of the data-driven model. Results are based on 50,000 realizations of each model. Results are aligned at the epidemic peak, which corresponds to time $t=0$. Inset shows the logarithm of the mean daily incidence of new influenza infections over time, which does not follow a linear trend. (B) Mean $R\left(t\right)$ of data-driven and homogeneous models. The colored area shows the density distribution of $R\left(t\right)$ values obtained in the single realizations of the data-driven model. (C) The three lines represent the mean $Tg\left(t\right)$ of data-driven and homogeneous models. The colored area shows the density distribution of $Tg\left(t\right)$ values obtained in the single realizations of the data-driven model. The horizontal dotted gray line represent the constant value of the duration of the infectious period.

Fig. 3.

Layer-specific patterns. (A) Mean $R\left(t\right)$ for the data-driven model in the four layers. The colored area shows the density distribution of $R\left(t\right)$ values obtained in the single realizations. (B) Mean $Tg\left(t\right)$ for the data-driven model in the four layers. The colored area shows the density distribution of $Tg\left(t\right)$ values obtained in the single realizations.

Fig. 4.

The 2009 H1N1 influenza pandemic in Italy. (A) Seroprevalence rates by age as observed in a serosurvey conducted at the end of the 2009 H1N1 influenza pandemic in Italy (55) and as estimated by the calibrated model. (B) Epidemic growth rate over time $r\left(t\right)$ as estimated from the weekly incidence of new ILI cases in Italy over the course of the 2009 H1N1 influenza pandemic and the best-fitting linear model from week 35 to week 41 in 2009 (scale on the left axis). Weekly incidence of new ILI cases in Italy over the course of the 2009 H1N1 pandemic (scale on the right axis). Data are available at the ISS Influnet website (old.iss.it/flue/). Note that, over the period from week 35 to week 51 in 2009, schools were regularly open in Italy. (C) Temporal pattern of the mean weekly exponential epidemic growth rate ($r$) resulting from the analysis of the data-driven model calibrated on the 2009 H1N1 influenza seroprevalence data. The colored area shows the density distribution of $r\left(t\right)$ values obtained in the single realizations of the data-driven model.

Fig. 5.

Estimation of $R\left(t\right)$. (A) Daily $R\left(t\right)$ as inferred from the daily incidence of new infections for one stochastic model realization. $Tg$ is assumed to be exponentially distributed with an average of 3 d. (B) The same as A but the distribution of $Tg$ has been derived from the analysis of the transmission tree of the selected model simulation. (C) The same as A but using the distribution of $Tg$ over time as derived from the analysis of the transmission tree of the selected model simulation. The goodness of the estimate of $R\left(t\right)$ increases with a more precise knowledge of the generation time value and distribution.