Frequency-dependent decoupling of domain-wall motion and lattice strain in bismuth ferrite

Abstract

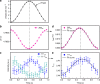
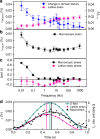
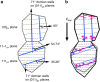
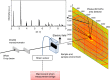
Dynamics of domain walls are among the main features that control strain mechanisms in ferroic materials. Here, we demonstrate that the domain-wall-controlled piezoelectric behaviour in multiferroic BiFeO₃ is distinct from that reported in classical ferroelectrics. In situ X-ray diffraction was used to separate the electric-field-induced lattice strain and strain due to displacements of non-180° domain walls in polycrystalline BiFeO₃ over a wide frequency range. These piezoelectric strain mechanisms have opposing trends as a function of frequency. The lattice strain increases with increasing frequency, showing negative piezoelectric phase angle (i.e., strain leads the electric field), an unusual feature so far demonstrated only in the total macroscopic piezoelectric response. Domain-wall motion exhibits the opposite behaviour, it decreases in magnitude with increasing frequency, showing more common positive piezoelectric phase angle (i.e., strain lags behind the electric field). Charge redistribution at conducting domain walls, oriented differently in different grain families, is demonstrated to be the cause.

Fig. 1

X-ray diffraction results. a Integrated segment of diffraction images of BiFeO₃ driven at 6 kV mm⁻¹ and 1 Hz cyclic electric field (see Methods). Insets indicate profile fitting using Gaussian peak functions on b 110_pc, c 111_pc, and d 200_pc, enabling the extraction of peak position, 2θ, and intensities of these individual single and double peaks

Fig. 2

Strain response to sinusoidal electric field. a Sinusoidal electric field, E, demonstrated for the 1 Hz measurement; b 200_pc peak position, 2θ; c intensities of 111_pc/11$\overline{1}$_pc reflections, and calculated d 200_pc lattice strain, ε₂₀₀; and e non-180° 111_pc domain texture, f₁₁₁. The error bars arise from profile fitting using Gaussian peak functions on individual single and double peaks. The dashed line is used here to indicate amplitude of electric field at ~0.5 s for the 1 Hz electric field

Fig. 3

Effect of electric field cycling as a function of frequency. a Calculated total lattice strain (magenta circles), ε_intrinsic, using equation (3), and change in non-180° 111_pc domain texture (blue diamonds), ∆f₁₁₁, using equation (2); b measured in situ macroscopic strain, ε_macro, by an optical displacement sensor coupled to the sample surface during XRD experiments (see Methods); c tangent of the piezoelectric phase angle, tanδ, of macroscopic strain (black squares) and lattice strain (magenta circles) during application of 6 kV mm⁻¹ unipolar sinusoidal electric field, E; and d time dependence of driving electric field (turquoise triangles), macroscopic strain (black squares), and lattice strain (magenta circles) responses demonstrated at 1 Hz, showing lagging (black straight line) and leading (magenta straight line) between strain and sinusoidal field signals. The errors of the lattice strain, change of non-180° 111_pc domain texture, macroscopic strain, and phase angle arise from sinusoidal curve fitting on these responses during application of driving cyclic field

Fig. 4

Schematic of two representative grains in poled BiFeO₃. a The diffraction planes and orientations of 71° domain walls, occurring on (011)_pc planes, in {100}_pc and {111}_pc grains. In {100}_pc grain (top grain), the 71° domain wall (solid blue lines) is perpendicular to the 100_pc diffracting planes (black dashed line). In the {111}_pc grain, the 71° domain walls separate 111_pc and 11$\overline{1}$_pc diffracting planes and form an angle of 35.26°. The angle between 71° domain walls in {100}_pc and {111}_pc grains is 54.74°; b charge distribution on conductive domain walls under applied external electric field, E_app = E₀sin(ωt). Charge redistribution rate is different for grains with different crystallographic orientations, i.e., {100}_pc and {111}_pc. Their dielectric permittivities, electrical conductivities and piezoelectric coefficients are thus different, represented by κ₁₀₀ and κ₁₁₁, σ₁₀₀ and σ₁₁₁, and d₁₀₀ and d₁₁₁, respectively. This will result in different effective fields in individual grains, represented by E₁₀₀ and E₁₁₁. The grain elongations upon field application, indicated by the solid black shapes, are due to the piezoelectric effect in the {100}_pc grain and non-180° domain wall motion in the {111}_pc grain

Fig. 5

Maxwell–Wagner analytical model and Rayleigh relationship calculations. a Redistributed effective fields, E₁₀₀ and E₁₁₁, in the two representative grains due to domain wall conductivity; b frequency dispersion and frequency-dependent decoupling of strain responses, ε₁₀₀ and ε₁₁₁, in {100}_pc and {111}_pc grain families calculated from effective field redistribution using piezoelectric equations; c phase angle, tan${\delta }_{{\epsilon }_{100}}$ and tan${\delta }_{{\epsilon }_{111}}$, of the strains in each grain family; and d time-dependent electric field and strains in two grains demonstrated for 1 Hz driving frequency. Calculations were made using equations (4)–(7) with relative permittivity κ₁₀₀ = 40, κ₁₁₁ = 30, relative conductivity σ₁₀₀ = 250, σ₁₁₁ = 100, piezoelectric coefficient d₁₀₀ = 45 pm V⁻¹, d₁₁₁ = 30 pm V⁻¹, and volume fractions of each grain v₁₀₀ = v₁₁₁ = 0.5. e Rayleigh phase angle due to the significant non-linearity at frequencies below ~1 Hz calculated from the experimental irreversible parameter, α (see Supplementary Figure 8)

Fig. 6

Schematic of the in situ XRD experimental setup. Samples were placed in the sample chamber and were bathed in silicon oil. The 2D image is obtained by a Dectris Pilatus3 X CdTe detector (see Methods) and the diffraction pattern is radially integrated from a wedge of the 2D diffraction image