Gravity estimation and verticality perception
- PMID: 30482332
- PMCID: PMC6295197
- DOI: 10.1016/B978-0-444-63916-5.00003-3
Gravity estimation and verticality perception
Abstract
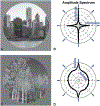
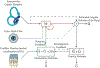
Gravity is a defining force that governs the evolution of mechanical forms, shapes and anchors our perception of the environment, and imposes fundamental constraints on our interactions with the world. Within the animal kingdom, humans are relatively unique in having evolved a vertical, bipedal posture. Although a vertical posture confers numerous benefits, it also renders us less stable than quadrupeds, increasing susceptibility to falls. The ability to accurately and precisely estimate our orientation relative to gravity is therefore of utmost importance. Here we review sensory information and computational processes underlying gravity estimation and verticality perception. Central to gravity estimation and verticality perception is multisensory cue combination, which serves to improve the precision of perception and resolve ambiguities in sensory representations by combining information from across the visual, vestibular, and somatosensory systems. We additionally review experimental paradigms for evaluating verticality perception, and discuss how particular disorders affect the perception of upright. Together, the work reviewed here highlights the critical role of multisensory cue combination in gravity estimation, verticality perception, and creating stable gravity-centered representations of our environment.
Keywords: cue disambiguation; cue integration; gravity; multisensory; reference frames; upright; verticality.
Copyright © 2018 Elsevier B.V. All rights reserved.
Figures


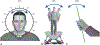
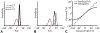

References
-
- Akbarian S, Grusser OJ, Guldin WO (1992). Thalamic connections of the vestibular cortical fields in the squirrel monkey. J Comp Neurol 326: 423–441. - PubMed
-
- Anastasopoulos D, Haslwanter T, Bronstein A et al. (1997). Dissociation between the perception of body verticality and the visual vertical in acute peripheral vestibular disorder in humans. Neurosci Lett 233: 151–153. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Medical

