The Anatomy of Inference: Generative Models and Brain Structure
- PMID: 30483088
- PMCID: PMC6243103
- DOI: 10.3389/fncom.2018.00090
The Anatomy of Inference: Generative Models and Brain Structure
Abstract
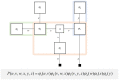
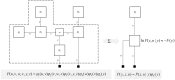
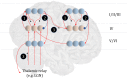
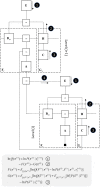
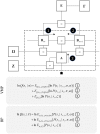
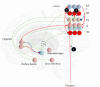
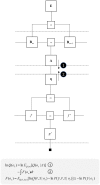
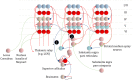
To infer the causes of its sensations, the brain must call on a generative (predictive) model. This necessitates passing local messages between populations of neurons to update beliefs about hidden variables in the world beyond its sensory samples. It also entails inferences about how we will act. Active inference is a principled framework that frames perception and action as approximate Bayesian inference. This has been successful in accounting for a wide range of physiological and behavioral phenomena. Recently, a process theory has emerged that attempts to relate inferences to their neurobiological substrates. In this paper, we review and develop the anatomical aspects of this process theory. We argue that the form of the generative models required for inference constrains the way in which brain regions connect to one another. Specifically, neuronal populations representing beliefs about a variable must receive input from populations representing the Markov blanket of that variable. We illustrate this idea in four different domains: perception, planning, attention, and movement. In doing so, we attempt to show how appealing to generative models enables us to account for anatomical brain architectures. Ultimately, committing to an anatomical theory of inference ensures we can form empirical hypotheses that can be tested using neuroimaging, neuropsychological, and electrophysiological experiments.
Keywords: Bayesian; active inference; generative model; message passing; neuroanatomy; predictive processing.
Figures



Similar articles
-
Neuronal message passing using Mean-field, Bethe, and Marginal approximations.Sci Rep. 2019 Feb 13;9(1):1889. doi: 10.1038/s41598-018-38246-3. Sci Rep. 2019. PMID: 30760782 Free PMC article.
-
The Markov blanket trick: On the scope of the free energy principle and active inference.Phys Life Rev. 2021 Dec;39:49-72. doi: 10.1016/j.plrev.2021.09.001. Epub 2021 Sep 14. Phys Life Rev. 2021. PMID: 34563472 Review.
-
Extended Variational Message Passing for Automated Approximate Bayesian Inference.Entropy (Basel). 2021 Jun 26;23(7):815. doi: 10.3390/e23070815. Entropy (Basel). 2021. PMID: 34206724 Free PMC article.
-
Generalised free energy and active inference.Biol Cybern. 2019 Dec;113(5-6):495-513. doi: 10.1007/s00422-019-00805-w. Epub 2019 Sep 27. Biol Cybern. 2019. PMID: 31562544 Free PMC article.
-
Computational Neuropsychology and Bayesian Inference.Front Hum Neurosci. 2018 Feb 23;12:61. doi: 10.3389/fnhum.2018.00061. eCollection 2018. Front Hum Neurosci. 2018. PMID: 29527157 Free PMC article. Review.
Cited by
-
An Active Inference Account of Skilled Anticipation in Sport: Using Computational Models to Formalise Theory and Generate New Hypotheses.Sports Med. 2022 Sep;52(9):2023-2038. doi: 10.1007/s40279-022-01689-w. Epub 2022 May 3. Sports Med. 2022. PMID: 35503403 Free PMC article. Review.
-
Time-consciousness in computational phenomenology: a temporal analysis of active inference.Neurosci Conscious. 2023 Mar 17;2023(1):niad004. doi: 10.1093/nc/niad004. eCollection 2023. Neurosci Conscious. 2023. PMID: 36937108 Free PMC article.
-
Active Inference, Epistemic Value, and Uncertainty in Conceptual Disorganization in First-Episode Schizophrenia.Schizophr Bull. 2023 Mar 22;49(Suppl_2):S115-S124. doi: 10.1093/schbul/sbac125. Schizophr Bull. 2023. PMID: 36946528 Free PMC article.
-
Subjective signal strength distinguishes reality from imagination.Nat Commun. 2023 Mar 23;14(1):1627. doi: 10.1038/s41467-023-37322-1. Nat Commun. 2023. PMID: 36959279 Free PMC article.
-
Embodied Object Representation Learning and Recognition.Front Neurorobot. 2022 Apr 14;16:840658. doi: 10.3389/fnbot.2022.840658. eCollection 2022. Front Neurorobot. 2022. PMID: 35496899 Free PMC article.
References
Publication types
Grants and funding
LinkOut - more resources
Full Text Sources
Miscellaneous

