Suppressing bursting synchronization in a modular neuronal network with synaptic plasticity

Abstract

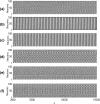
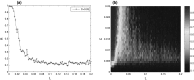
Excessive synchronization of neurons in cerebral cortex is believed to play a crucial role in the emergence of neuropsychological disorders such as Parkinson's disease, epilepsy and essential tremor. This study, by constructing a modular neuronal network with modified Oja's learning rule, explores how to eliminate the pathological synchronized rhythm of interacted busting neurons numerically. When all neurons in the modular neuronal network are strongly synchronous within a specific range of coupling strength, the result reveals that synaptic plasticity with large learning rate can suppress bursting synchronization effectively. For the relative small learning rate not capable of suppressing synchronization, the technique of nonlinear delayed feedback control including differential feedback control and direct feedback control is further proposed to reduce the synchronized bursting state of coupled neurons. It is demonstrated that the two kinds of nonlinear feedback control can eliminate bursting synchronization significantly when the control parameters of feedback strength and feedback delay are appropriately tuned. For the former control technique, the control domain of effective synchronization suppression is similar to a semi-elliptical domain in the simulated parameter space of feedback strength and feedback delay, while for the latter one, the effective control domain is similar to a fan-shaped domain in the simulated parameter space.

Keywords: Bursting synchronization; Modular neuronal network; Nonlinear delayed feedback control; Synaptic plasticity.

Fig. 1

a The order parameter $R$ and b the variance $Var(X)$ as a function of coupling strength $C$ when the modular network is absence of synaptic plasticity and nonlinear delayed feedback control. It is seen that bursting synchronization can be induced by large coupling. When calculating $R$ and $Var(X)$, the solution of Eq. (2) for the first 3000 times is considered as transient state

Fig. 2

Spatiotemporal patterns of the modular network when a $C=0.0$, $L=0.0$, b $C=0.03$, $L=0.0$ c $C=0.03$, $L=0.01$, d $C=0.03$, $L=0.02$, e $C=0.03$, $L=0.08$ and f $C=0.03$, $L=0.18$. As $L$ increases, the synchronized patterns of the modular network are gradually destroyed

Fig. 3

a The order parameter $R$ as a function of learning rate $L$ when $C=0.03$. b The contour plot of order parameter as a function of coupling $C$ and learning rate $L$. It is seen that larger learning rate can suppress bursting synchronization effectively when the coupling is within a specific range. When calculating $R$, the solution of Eq. (2) for the first 3000 times is considered as transient state

Fig. 4

The membrane potential of two connected neurons in the considered neuronal network, the corresponding synaptic weights and the ensemble-averaged synaptic weights of the whole network. The left three figures for the case of C = 0.03, L = 0.01 and the right three ones for the case of C = 0.03, L = 0.18

Fig. 5

The evolution of (a) mean filed $X(n)$ and (b) membrane potential of two arbitrary neurons when the nonlinear differential feedback with $K=3.6,\tau =90$ is switched on at time $n=4000$. (c) Suppression coefficient $S$ versus feedback delay $\tau$ when $K=3.6$. When calculating $S$, the solution of Eq. (2) for the first 5000 times is considered as transient state. It can be seen that bursting synchronization can be suppressed when feedback delay is appropriately tuned

Fig. 6

Mean field of the modular network for different feedback delay $\tau$ with $K=3.6$: a $\tau =0$, b $\tau =50$, c $\tau =80$, d $\tau =110$. It can be seen that bursting synchronization can be suppressed when feedback delay is appropriately tuned

Fig. 7

a Suppression coefficient $S$ versus feedback delay $\tau$ for different $K$. b The contour plot of suppression coefficient $S$ versus $\tau$ and $K$. When calculating $S$, the solution of Eq. (2) for the first 5000 times is considered as transient state. The control domain of effective synchronization suppression by differential feedback control is approximately characterized by a semi-elliptical domain in the simulated parameter space

Fig. 8

The evolution of (a) mean filed $X(n)$ and (b) membrane potential of two arbitrary neurons when the nonlinear direct feedback with $K=-3.6,\tau =30$ is switched on at time $n=4000$. (c) Suppression coefficient $S$ versus feedback delay $\tau$ when $K=-3.6$. When calculating $S$, the solution of Eq. (2) for the first 5000 times is considered as transient state. It can be seen that bursting synchronization can be suppressed when feedback delay is appropriately tuned

Fig. 9

Mean field of the modular network for different feedback delay $\tau$ with $K=-3.6$: a $\tau =0$, b $\tau =50$, c $\tau =80$, d $\tau =150$. It can be seen that bursting synchronization can be suppressed when feedback delay is appropriately tuned

Fig. 10

a Suppression coefficient $S$ versus feedback delay $\tau$ for different $K$. b The contour plot of suppression coefficient $S$ versus $\tau$ and $K$. When calculating $S$, the solution of Eq. (2) for the first 5000 times is considered as transient state. The control domain of effective synchronization suppression by direct feedback control is similar to a fan-shaped region in the simulated parameter space