A computational investigation of lift generation and power expenditure of Pratt's roundleaf bat (Hipposideros pratti) in forward flight

Abstract

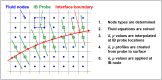
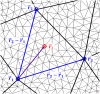
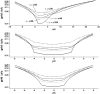
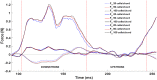
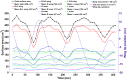
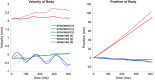
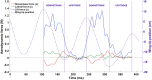
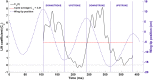
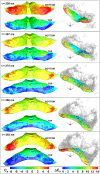
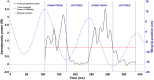
The aerodynamic mechanisms of bat flight have been studied using a numerical approach. Kinematic data acquired using a high resolution motion capture system was employed to simulate the unsteady air flow around a bat's wings. A flapping bat wing contains many degrees of freedom, which make 3D motion tracking challenging. In order to overcome this challenge, an optical motion capture system of 21 cameras was used to reduce wing self-occlusion. Over the course of a meter-long flight, 108 discrete marker points on the bat's wings (Pratt's roundleaf bat, Hipposideros pratti) were tracked. The time evolution of the surface of each wing was computationally reconstructed in 3D space. The resulting kinematic model was interfaced with an unsteady incompressible flow solver using the immersed boundary method (IBM) and large eddy simulation (LES). Verification and validation of the flow simulation were conducted to establish accuracy. The aerodynamic forces calculated from the simulation compared well to the forces theoretically needed to sustain the observed flight trajectory. The transient flow field generated by the simulation allowed for the direct calculation of lift, drag, and power output of the bat during flight. The mean lift coefficient was found to be 3.21, and the flap cycle averaged aerodynamic power output was 1.05 W. Throughout the flap cycle, the planform area of the wings varied up to 46% between the largest and smallest values. During the upstroke, wing rotation was found to mitigate negative lift thereby improving overall flight efficiency. The high resolution motion capture and flow simulation framework presented here has the potential to facilitate the understanding of complex bat flight aerodynamics for both straight and maneuvering flight modes.

Fig 1. Motion capture system, consisting of 21 GoPro cameras inside a 1.2 x 1.2 meter cross section flight tunnel.

The bat was trained to fly through the tunnel and land on the cork perch shown.

Fig 2. Small white markers were placed on each bat wing to aid 3D reconstruction of the wing kinematics during flight.

Fig 3. Five snapshots of the bat in flight along with the corresponding 3D reconstructed data.

The radial distortion of the camera lens slightly changes the visual perspective of the bat in the video, however that is mathematically accounted for during the camera calibration process. In the digital reconstruction, the magenta trace is the path of the bat body, and the green traces are the path of the wing tips.

Fig 4. Immersed boundary method setup.

A thin interface (red) is embedded into the background fluid grid. The no slip boundary condition is enforced on the interface by applying an appropriate velocity and pressure values to the IB nodes (green) at each time step. The property values at each IB node are determined by creating velocity profiles between the fluid nodes and the no slip surface.

Fig 5. Wing surface mesh viewed from above during the most outstretched point of the downstroke.

The coarse and fine wing surface meshes are showed overlaid with the fluid grid in the background. The vertices of the coarse triangular mesh correspond to the white marker points on the bat wings.

Fig 6. A given control triangle consists of three control points, and several interior points.

The area inside the triangle is parameterized into a 2D surface, where every location is described by a unique pair of α and β values. As the wing flaps, the triangles deform and the locations of the interiors points are updated accordingly.

Fig 7. The full fluid grid viewed from above shows the refined region in the vicinity of the bat.

The y- and z-faces of the domain reflect the physical size of the experimental flight tunnel, while the x-faces were positioned sufficiently far from the bat to avoid interference from the boundary.

Fig 8. The grid spacing distribution for the five grids described in Table 2.

Fig 9. Comparison of the unsteady fluid force components for a complete flap cycle.

Some discrepancy can be observed between the coarsest (blue) and finest (black) grids, however the two finest grids—50 and 100 cells per chord—show close agreement throughout the flap cycle for all three force components.

Fig 10. Nine frames sampled from two complete flap cycles are shown.

t/T is the normalized time starting from the downstroke, and normalized by the flap period of 138 ms.

Fig 11. The total surface area variation of the bat wings, tail, and body is shown over the course of the flight (solid black).

For context, the wing tip positions are shown (dotted black) to indicate the upstroke and downstroke.

Fig 12

Left: Comparison of the simulated and observed velocity in x, y, and z. Right: The simulated flight trajectory is compared to the observed flight trajectory. The vertical and lateral predictions are very close, however the streamwise position is under predicted by 15 cm.

Fig 13. The time variation of aerodynamic force is shown along with the wing tip position for context.

The peak lift force was around 1.2 N, and the cycle averaged mean was 0.525 N. The streamwise and lateral forces were both close to zero since the flight was approximately straight and level.

Fig 14. The lift coefficient is plotted along with the wing tip location for context.

The mean value was C_L = 3.21.

Fig 15

Top: Coherent vorticity (iso-surfaces of Δ-criterion) is shown along with the wing surface pressure at four snapshots throughout the flap cycle. Bottom: Flight velocity, planform area, wing span, aerodynamic force, and aerodynamic power are plotted with each of the four snapshot locations indicated. (a) the top of the upstroke, (b) the point of maximum lift production, (c) the bottom of the downstroke, and (d) the midpoint of the upstroke.

Fig 16

Left: Aerodynamic pressure on the top and bottom of the bat wing is shown at 5 instances during the downstroke. Right: Pressure difference is shown on the wing surface with iso-surfaces of coherent vorticity.

Fig 17. Aerodynamic power is plotted for two complete flap cycles along with wing tip position for context.

Power expenditure was maximum during the second half of each downstroke at around 2.5 to 3.5 Watts. The cycle averaged value over both flaps was 1.05 Watts.