Statistical methodology for constructing gestational age-related charts using cross-sectional and longitudinal data: The INTERGROWTH-21st project as a case study

Abstract

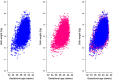
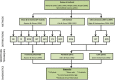
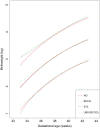
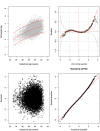
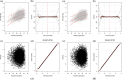
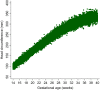
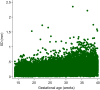
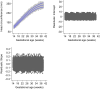
Most studies aiming to construct reference or standard charts use a cross-sectional design, collecting one measurement per participant. Reference or standard charts can also be constructed using a longitudinal design, collecting multiple measurements per participant. The choice of appropriate statistical methodology is important as inaccurate centiles resulting from inferior methods can lead to incorrect judgements about fetal or newborn size, resulting in suboptimal clinical care. Reference or standard centiles should ideally provide the best fit to the data, change smoothly with age (eg, gestational age), use as simple a statistical model as possible without compromising model fit, and allow the computation of Z-scores from centiles to simplify assessment of individuals and enable comparison with different populations. Significance testing and goodness-of-fit statistics are usually used to discriminate between models. However, these methods tend not to be useful when examining large data sets as very small differences are statistically significant even if the models are indistinguishable on actual centile plots. Choosing the best model from amongst many is therefore not trivial. Model choice should not be based on statistical considerations (or tests) alone as sometimes the best model may not necessarily offer the best fit to the raw data across gestational age. In this paper, we describe the most commonly applied methodologies available for the construction of age-specific reference or standard centiles for cross-sectional and longitudinal data: Fractional polynomial regression, LMS, LMST, LMSP, and multilevel regression methods. For illustration, we used data from the INTERGROWTH-21^st Project, ie, newborn weight (cross-sectional) and fetal head circumference (longitudinal) data as examples.

Keywords: cross-sectional; human growth; longitudinal; statistical methodology.

Figure 1

Scatter plot of birthweight measurements according to gestational age for boys (left, blue), girls (middle, pink), and girls and boys superimposed (right) [Colour figure can be viewed at wileyonlinelibrary.com]

Figure 2

A summary of the most commonly used statistical methodology for analysing growth data. BCCG, Box‐Cox Cole and Green; BCPE, Box‐Cox power exponential distribution; BCT, Box‐Cox t‐distribution; NO, normal distribution; PE, power exponential; SEP3, skew exponential power type 3; ST3, skew t‐distribution type 3; Q‐Q, quantile‐quantile [Colour figure can be viewed at wileyonlinelibrary.com]

Figure 3

A comparison of fitted centiles for Male birthweight using fractional polynomial regression of selected distributions (ie, normal distribution, Box‐Cox Cole and Green distribution (BCCG), skew exponential power type 3 (ST3)), and the LMS method (LMS (BCCG)) [Colour figure can be viewed at wileyonlinelibrary.com]

Figure 4

The fractional polynomial regression method: fractional polynomial fit of a two‐parameter model assuming a normal distribution (two powers for the mean and one for the SD) for male birthweight (Model: M1_B, Table 2). The plot shows (A) the fitted 3^rd, 50^th, and 97^th smoothed centiles according to gestational age (top left panel), (B) a worm plot (top right panel), (C) a scatter plot of the residuals according to gestational age (bottom left panel), and (D) normal quantile‐quantile (Q‐Q) plots of the distribution of Z‐scores (bottom right panel) [Colour figure can be viewed at wileyonlinelibrary.com]

Figure 5

Panel A is MALES and panel B is FEMALES the fractional polynomial regression method: fractional polynomial fit of a four‐parameter model assuming a skew t‐distribution type 3 distribution (two powers for the mean, one for the SD, one for skewness, and one for kurtosis) for male birthweight (Model: M6_B, Table 2). The plot shows (a) the fitted 3^rd, 50^th, and 97^th smoothed centiles according to gestational age (top left panel), (b) a worm plot (top right panel), (c) a scatter plot of the residuals according to gestational age (bottom left panel), and (d) normal quantile‐quantile (Q‐Q) plots of the distribution of Z‐scores (bottom right panel) [Colour figure can be viewed at wileyonlinelibrary.com]

Figure 6

Scatter plots of the raw fetal head circumference measurements by gestational age for all of the sites combined [Colour figure can be viewed at wileyonlinelibrary.com]

Figure 7

Variance of each set of triplicate measurements at each visit for all women according to gestational age [Colour figure can be viewed at wileyonlinelibrary.com]

Figure 8

Fitted 3^rd, 50^th, and 97^th smoothed centile curves (dashed blue lines) for fetal head circumference (mm) by ultrasound according to gestational age (weeks), showing the actual observations (open grey circles) (top left), plot of intercept residuals against gestational age (top right), and slope residuals against gestational age (bottom left), of a three‐level random intercept and slope multilevel model applied to all fetal head circumference triplicate measurements taken at each visit [Colour figure can be viewed at wileyonlinelibrary.com]