Radiative transfer in a discrete random medium adjacent to a half-space with a rough interface

Abstract

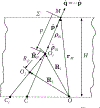
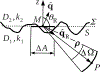
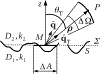
For a macroscopically plane-parallel discrete random medium, the boundary conditions for the specific coherency dyadic at a rough interface are derived. The derivation is based on a modification of the Twersky approximation for a scattering system consisting of a group of particles and the rough surface, and reduces to the solution of the scattering problem for a rough surface illuminated by a plane electromagnetic wave propagating in a discrete random medium with non-scattering boundaries. In a matrix-form setting, the boundary conditions for the specific coherency dyadic imply the boundary conditions for specific intensity column vectors which in turn, yield the expressions for the reflection and transmission matrices. The derived expressions are shown to be identical to those obtained by applying a phenomenological approach based on a facet model to the solution of the scattering problem for a rough surface illuminated by a plane electromagnetic wave.

Figure 1:

Left: scattering geometry of a discrete random layer with a non-scattering lower plane boundary z = 0 and an upper rough surface boundary S. Right: local coordinate system attached to M .

Figure 2:

Geometry for computing the configuration average.

Figure 3:

Ladder approximation for the coherency dyadic.

Figure 4:

Incidence and reflection directions $\widehat{\mathbf{q}}$ and ${\widehat{\mathbf{q}}}_{\mathrm{R}}$, respectively, and the area of the illuminated surface ΔA.

Figure 5:

Ladder approximation of $\langle {\mathbf{E}}_{\text{R}}^{\infty }\otimes {\mathbf{E}}_{\mathbf{R}}^{\infty \star }\rangle$.

Figure 6:

Incidence and transmission directions $\widehat{\mathbf{q}}$ and ${\widehat{\mathbf{q}}}_{\mathbf{T}}$, respectively, and the area of the illuminated surface ΔA.