Optimal and near-optimal exponent-pairs for the Bertalanffy-Pütter growth model

Abstract

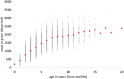
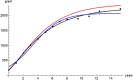
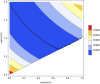
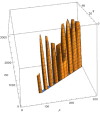
The Bertalanffy-Pütter growth model describes mass m at age t by means of the differential equation dm/dt = p * m ^a - q * m^b . The special case using the von Bertalanffy exponent-pair a = 2/3 and b = 1 is most common (it corresponds to the von Bertalanffy growth function VBGF for length in fishery literature). Fitting VBGF to size-at-age data requires the optimization of three model parameters (the constants p, q, and an initial value for the differential equation). For the general Bertalanffy-Pütter model, two more model parameters are optimized (the pair a < b of non-negative exponents). While this reduces bias in growth estimates, it increases model complexity and more advanced optimization methods are needed, such as the Nelder-Mead amoeba method, interior point methods, or simulated annealing. Is the improved performance worth these efforts? For the case, where the exponent b = 1 remains fixed, it is known that for most fish data any exponent a < 1 could be used to model growth without affecting the fit to the data significantly (when the other parameters were optimized). We hypothesized that the optimization of both exponents would result in a significantly better fit of the optimal growth function to the data and we tested this conjecture for a data set (20,166 fish) about the mass-growth of Walleye (Sander vitreus), a fish from Lake Erie, USA. To this end, we assessed the fit on a grid of 14,281 exponent-pairs (a, b) and identified the best fitting model curve on the boundary a = b of the grid (a = b = 0.686); it corresponds to the generalized Gompertz equation dm/dt = p * m^a - q * ln(m) * m^a . Using the Akaike information criterion for model selection, the answer to the conjecture was no: The von Bertalanffy exponent-pair model (but not the logistic model) remained parsimonious. However, the bias reduction attained by the optimal exponent-pair may be worth the tradeoff with complexity in some situations where predictive power is solely preferred. Therefore, we recommend the use of the Bertalanffy-Pütter model (and of its limit case, the generalized Gompertz model) in natural resources management (such as in fishery stock assessments), as it relies on careful quantitative assessments to recommend policies for sustainable resource usage.

Keywords: Akaike information criterion; Bertalanffy–Pütter differential equation; Region of near-optimality.

Figure 1. Weight-at-age and average weight (red dots) of male Walleye from Lake Erie.

Figure 2. Comparison with the data of the growth curve using the Bertalanffy exponent-pair (red), the logistic exponent pair (blue) and of the best fitting growth curve (black); parameter values as in Table 2.

Figure 3. Contour plot of the optimal SSE on a grid of exponent-pairs with distance 0.01 between adjacent points and for each exponent a, plot of the exponent-pair with smallest SSE (black dots).

Figure 4. Plot of the Akaike weights for exponent-pairs with b = 1, using the least AIC amongst generalized Bertalanffy-models (red) and the least AIC amongst all considered models (blue); all AICs using K = 4.

Figure 5. Plot of the grid points a < b with AIC below AIC of the best fitting model (green; the AIC of the best fitting model was higher due to the penalty for an additional parameter) and with acceptable fit (red). The Bertalanffy and the logistic exponent-pairs are displayed in yellow.

Figure 6. Plot of part of the region of exponents m_0 p, q for model (2) with the optimal exponent a = 0.686028, where SSE does not exceed 10⁷.