Traveling pulse emerges from coupled intermittent walks: A case study in sheep
- PMID: 30517114
- PMCID: PMC6281248
- DOI: 10.1371/journal.pone.0206817
Traveling pulse emerges from coupled intermittent walks: A case study in sheep
Abstract
Monitoring small groups of sheep in spontaneous evolution in the field, we decipher behavioural rules that sheep follow at the individual scale in order to sustain collective motion. Individuals alternate grazing mode at null speed and moving mode at walking speed, so cohesive motion stems from synchronising when they decide to switch between the two modes. We propose a model for the individual decision making process, based on switching rates between stopped / walking states that depend on behind / ahead locations and states of the others. We parametrize this model from data. Next, we translate this (microscopic) individual-based model into its density-flow (macroscopic) equations counterpart. Numerical solving these equations display a traveling pulse propagating at constant speed even though each individual is at any moment either stopped or walking. Considering the minimal model embedded in these equations, we derive analytically the steady shape of the pulse (sech square). The parameters of the pulse (shape and speed) are expressed as functions of individual parameters. This pulse emerges from the non linear coupling of start/stop individual decisions which compensate exactly for diffusion and promotes a steady ratio of walking / stopped individuals, which in turn determines the traveling speed of the pulse. The system seems to converge to this pulse from any initial condition, and to recover the pulse after perturbation. This gives a high robustness to this coordination mechanism.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures

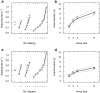
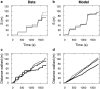


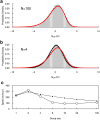


Similar articles
-
Intermittent collective dynamics emerge from conflicting imperatives in sheep herds.Proc Natl Acad Sci U S A. 2015 Oct 13;112(41):12729-34. doi: 10.1073/pnas.1503749112. Epub 2015 Sep 28. Proc Natl Acad Sci U S A. 2015. PMID: 26417082 Free PMC article.
-
Flow control by means of a traveling curvature wave in fishlike escape responses.Phys Rev E Stat Nonlin Soft Matter Phys. 2011 Nov;84(5 Pt 2):056312. doi: 10.1103/PhysRevE.84.056312. Epub 2011 Nov 18. Phys Rev E Stat Nonlin Soft Matter Phys. 2011. PMID: 22181503
-
Models for temporal-spatial parameters in walking with cadence ratio as the independent variable.Med Biol Eng Comput. 2019 Apr;57(4):877-886. doi: 10.1007/s11517-018-1919-8. Epub 2018 Nov 21. Med Biol Eng Comput. 2019. PMID: 30465322 Free PMC article. Clinical Trial.
-
Lower limb sagittal kinematic and kinetic modeling of very slow walking for gait trajectory scaling.PLoS One. 2018 Sep 17;13(9):e0203934. doi: 10.1371/journal.pone.0203934. eCollection 2018. PLoS One. 2018. PMID: 30222772 Free PMC article.
-
Effects of random motion in traveling and grazing herds.J Theor Biol. 2018 Nov 7;456:168-174. doi: 10.1016/j.jtbi.2018.08.012. Epub 2018 Aug 7. J Theor Biol. 2018. PMID: 30096404
Cited by
-
Swimming ability and flagellar motility of sperm packets of the volvocine green alga Pleodorina starrii.PLoS One. 2024 Jul 18;19(7):e0287561. doi: 10.1371/journal.pone.0287561. eCollection 2024. PLoS One. 2024. PMID: 39024288 Free PMC article.
References
-
- Sumpter DJT. The principles of collective animal behaviour. Philos Trans R Soc Lond B Biol Sci. 2006;361(1465):5–22. 10.1098/rstb.2005.1733 - DOI - PMC - PubMed
-
- Eftimie R, de Vries G, Lewis Ma. Complex spatial group patterns result from different animal communication mechanisms. Proc Natl Acad Sci U S A. 2007;104(17):6974–6979. 10.1073/pnas.0611483104 - DOI - PMC - PubMed
-
- Tindall MJ, Maini PK, Porter SL, Armitage JP. Overview of mathematical approaches used to model bacterial chemotaxis II: Bacterial populations. Bulletin of Mathematical Biology. 2008;70(6):1570–1607. 10.1007/s11538-008-9322-5 - DOI - PubMed
-
- Saragosti J, Calvez V, Bournaveas N, Buguin A, Silberzan P, Perthame B. Mathematical description of bacterial traveling pulses. PLoS Comput Biol. 2010;6(8). 10.1371/journal.pcbi.1000890 - DOI - PMC - PubMed
-
- Sumpter DJT. Collective Animal Behavior. Princeton, NJ: Princeton University Press; 2010.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources

