Community dynamics and sensitivity to model structure: towards a probabilistic view of process-based model predictions
- PMID: 30518566
- PMCID: PMC6303789
- DOI: 10.1098/rsif.2018.0741
Community dynamics and sensitivity to model structure: towards a probabilistic view of process-based model predictions
Abstract
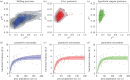
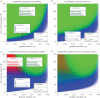
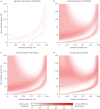
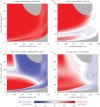
Statistical inference and mechanistic, process-based modelling represent two philosophically different streams of research whose primary goal is to make predictions. Here, we merge elements from both approaches to keep the theoretical power of process-based models while also considering their predictive uncertainty using Bayesian statistics. In environmental and biological sciences, the predictive uncertainty of process-based models is usually reduced to parametric uncertainty. Here, we propose a practical approach to tackle the added issue of structural sensitivity, the sensitivity of predictions to the choice between quantitatively close and biologically plausible models. In contrast to earlier studies that presented alternative predictions based on alternative models, we propose a probabilistic view of these predictions that include the uncertainty in model construction and the parametric uncertainty of each model. As a proof of concept, we apply this approach to a predator-prey system described by the classical Rosenzweig-MacArthur model, and we observe that parametric sensitivity is regularly overcome by structural sensitivity. In addition to tackling theoretical questions about model sensitivity, the proposed approach can also be extended to make probabilistic predictions based on more complex models in an operational context. Both perspectives represent important steps towards providing better model predictions in biology, and beyond.
Keywords: Bayesian statistics; community dynamics; model predictions; predation; structural sensitivity.
© 2018 The Author(s).
Conflict of interest statement
We have no competing interests.
Figures
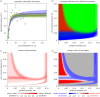
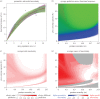
References
-
- Anderson TR. 2010. Progress in marine ecosystem modelling and the ‘unreasonable effectiveness of mathematics’. J. Mar. Sys. 81, 4–11. (10.1016/j.jmarsys.2009.12.015) - DOI
-
- Pennekamp F, Adamson MW, Petchey OL, Poggiale JC, Aguiar M, Kooi BW, Botkin DB, DeAngelis DL. 2017. The practice of prediction: what can ecologists learn from applied, ecology-related fields? Ecol. Complexity 32, 156–167. (10.1016/j.ecocom.2016.12.005) - DOI
-
- Rosenzweig ML, MacArthur RH. 1963. Graphical representation and stability conditions of predator–prey interaction. Am. Nat. 97, 209–223. (10.1086/282272) - DOI
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Research Materials
