Robust forecast aggregation

Abstract

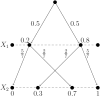
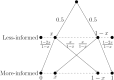
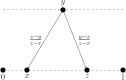
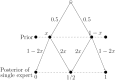
Bayesian experts who are exposed to different evidence often make contradictory probabilistic forecasts. An aggregator, ignorant of the underlying model, uses this to calculate his or her own forecast. We use the notions of scoring rules and regret to propose a natural way to evaluate an aggregation scheme. We focus on a binary state space and construct low regret aggregation schemes whenever there are only two experts that either are Blackwell-ordered or receive conditionally independent and identically distributed (i.i.d.) signals. In contrast, if there are many experts with conditionally i.i.d. signals, then no scheme performs (asymptotically) better than a [Formula: see text] forecast.

Keywords: Blackwell-ordered information structure; conditionally independent information structure; information aggregation; one-shot regret minimization.

Fig. 1.

The martingale $X_1,X_2$.

Fig. 2.

The martingale of posteriors.

Fig. 3.

$M_{x,y,z}$, the extreme points of the class of martingales.

Fig. 4.

Distribution over priors and posteriors of a single agent.