Coherent chaos in a recurrent neural network with structured connectivity
- PMID: 30543634
- PMCID: PMC6307850
- DOI: 10.1371/journal.pcbi.1006309
Coherent chaos in a recurrent neural network with structured connectivity
Abstract
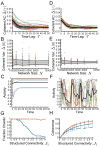
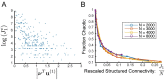
We present a simple model for coherent, spatially correlated chaos in a recurrent neural network. Networks of randomly connected neurons exhibit chaotic fluctuations and have been studied as a model for capturing the temporal variability of cortical activity. The dynamics generated by such networks, however, are spatially uncorrelated and do not generate coherent fluctuations, which are commonly observed across spatial scales of the neocortex. In our model we introduce a structured component of connectivity, in addition to random connections, which effectively embeds a feedforward structure via unidirectional coupling between a pair of orthogonal modes. Local fluctuations driven by the random connectivity are summed by an output mode and drive coherent activity along an input mode. The orthogonality between input and output mode preserves chaotic fluctuations by preventing feedback loops. In the regime of weak structured connectivity we apply a perturbative approach to solve the dynamic mean-field equations, showing that in this regime coherent fluctuations are driven passively by the chaos of local residual fluctuations. When we introduce a row balance constraint on the random connectivity, stronger structured connectivity puts the network in a distinct dynamical regime of self-tuned coherent chaos. In this regime the coherent component of the dynamics self-adjusts intermittently to yield periods of slow, highly coherent chaos. The dynamics display longer time-scales and switching-like activity. We show how in this regime the dynamics depend qualitatively on the particular realization of the connectivity matrix: a complex leading eigenvalue can yield coherent oscillatory chaos while a real leading eigenvalue can yield chaos with broken symmetry. The level of coherence grows with increasing strength of structured connectivity until the dynamics are almost entirely constrained to a single spatial mode. We examine the effects of network-size scaling and show that these results are not finite-size effects. Finally, we show that in the regime of weak structured connectivity, coherent chaos emerges also for a generalized structured connectivity with multiple input-output modes.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures



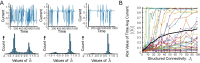


Similar articles
-
The connections between the frustrated chaos and the intermittency chaos in small Hopfield networks.Neural Netw. 2002 Dec;15(10):1197-204. doi: 10.1016/s0893-6080(02)00096-5. Neural Netw. 2002. PMID: 12425438
-
How single neuron properties shape chaotic dynamics and signal transmission in random neural networks.PLoS Comput Biol. 2019 Jun 10;15(6):e1007122. doi: 10.1371/journal.pcbi.1007122. eCollection 2019 Jun. PLoS Comput Biol. 2019. PMID: 31181063 Free PMC article.
-
Transition to chaos in random networks with cell-type-specific connectivity.Phys Rev Lett. 2015 Feb 27;114(8):088101. doi: 10.1103/PhysRevLett.114.088101. Epub 2015 Feb 23. Phys Rev Lett. 2015. PMID: 25768781 Free PMC article.
-
Chaotic recurrent neural networks for brain modelling: A review.Neural Netw. 2025 Apr;184:107079. doi: 10.1016/j.neunet.2024.107079. Epub 2024 Dec 27. Neural Netw. 2025. PMID: 39756119 Review.
-
Effects of Hebbian learning on the dynamics and structure of random networks with inhibitory and excitatory neurons.J Physiol Paris. 2007 Jan-May;101(1-3):136-48. doi: 10.1016/j.jphysparis.2007.10.003. Epub 2007 Oct 16. J Physiol Paris. 2007. PMID: 18042357 Review.
Cited by
-
Modulation of the dynamical state in cortical network models.Curr Opin Neurobiol. 2021 Oct;70:43-50. doi: 10.1016/j.conb.2021.07.004. Epub 2021 Aug 14. Curr Opin Neurobiol. 2021. PMID: 34403890 Free PMC article. Review.
-
Balanced networks under spike-time dependent plasticity.PLoS Comput Biol. 2021 May 12;17(5):e1008958. doi: 10.1371/journal.pcbi.1008958. eCollection 2021 May. PLoS Comput Biol. 2021. PMID: 33979336 Free PMC article.
-
Optimal noise level for coding with tightly balanced networks of spiking neurons in the presence of transmission delays.PLoS Comput Biol. 2022 Oct 17;18(10):e1010593. doi: 10.1371/journal.pcbi.1010593. eCollection 2022 Oct. PLoS Comput Biol. 2022. PMID: 36251693 Free PMC article.
-
Different eigenvalue distributions encode the same temporal tasks in recurrent neural networks.Cogn Neurodyn. 2023 Feb;17(1):257-275. doi: 10.1007/s11571-022-09802-5. Epub 2022 Apr 20. Cogn Neurodyn. 2023. PMID: 35469119 Free PMC article.
-
Large-scale neural recordings call for new insights to link brain and behavior.Nat Neurosci. 2022 Jan;25(1):11-19. doi: 10.1038/s41593-021-00980-9. Epub 2022 Jan 3. Nat Neurosci. 2022. PMID: 34980926 Review.
References
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

