Mixed effects approach to the analysis of the stepped wedge cluster randomised trial-Investigating the confounding effect of time through simulation

Abstract

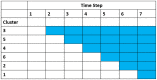
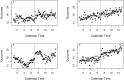
Background: A stepped wedge cluster randomised trial (SWCRT) is a multicentred study which allows an intervention to be rolled out at sites in a random order. Once the intervention is initiated at a site, all participants within that site remain exposed to the intervention for the remainder of the study. The time since the start of the study ("calendar time") may affect outcome measures through underlying time trends or periodicity. The time since the intervention was introduced to a site ("exposure time") may also affect outcomes cumulatively for successful interventions, possibly in addition to a step change when the intervention began.

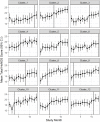
Methods: Motivated by a SWCRT of self-monitoring for bipolar disorder, we conducted a simulation study to compare model formulations to analyse data from a SWCRT under 36 different scenarios in which time was related to the outcome (improvement in mood score). The aim was to find a model specification that would produce reliable estimates of intervention effects under different scenarios. Nine different formulations of a linear mixed effects model were fitted to these datasets. These models varied in the specification of calendar and exposure times.

Results: Modelling the effects of the intervention was best accomplished by including terms for both calendar time and exposure time. Treating time as categorical (a separate parameter for each measurement time-step) achieved the best coverage probabilities and low bias, but at a cost of wider confidence intervals compared to simpler models for those scenarios which were sufficiently modelled by fewer parameters. Treating time as continuous and including a quadratic time term performed similarly well, with slightly larger variations in coverage probability, but narrower confidence intervals and in some cases lower bias. The impact of misspecifying the covariance structure was comparatively small.

Conclusions: We recommend that unless there is a priori information to indicate the form of the relationship between time and outcomes, data from SWCRTs should be analysed with a linear mixed effects model that includes separate categorical terms for calendar time and exposure time. Prespecified sensitivity analyses should consider the different formulations of these time effects in the model, to assess their impact on estimates of intervention effects.

Fig 1. Mean plots with 95% confidence intervals (C.I.) of the total HoNOS scores plotted against the calendar time (study months) at each CMHT for the OXTEXT-7 study.

Data to the left of the vertical line occurred before the intervention and data to the right after the intervention was introduced.

Fig 2. Graphical representation of the standard stepped wedge design intervention roll-out.

Fig 3. Four potential ways that an outcome can change as a function of time.

The dashed line represents when the intervention is introduced. See text for further details. a.) Step change, no time trend, b.) Linear trends in calendar and exposure time, c.) Step change, non-linear trend in calendar time, d.) Step change, linear trends in calendar and exposure time.

Fig 4. The simulated data under scenario D17: y_ik(t) = 14 + 2x_tk + 0.25t + 0.25d_tk.

The means and 95% confidence intervals are plotted against the time since the intervention was introduced. Data to the left of the vertical line occurred before the intervention and data to the right after the intervention was introduced.

Fig 5. The heat map shows the coverage probability of the intervention effect at six months exposure for the nine fitted models with CS correlation structure.

The heat map was very similar when the AR(1) structure was specified and for the time-averaged intervention effect. Values at the bottom of each column show the average coverage probability for each fitted model and the average width of the confidence interval for the intervention effect. Odd-numbered scenarios are simulated with ρ = -0.5 and even-numbered scenarios have ρ = 0.5.

Fig 6. Plot of mean bias and mean 95% confidence interval width over all datasets within each scenario for each fitted model for the estimate of the intervention effect at six months exposure.

Fig 7. Plot of mean bias and mean 95% confidence interval width over all datasets within each scenario for each fitted model for the estimate of the time-averaged intervention effect.

Fig 8. Plot of the mean of the MSE (mean square error) and mean BIC over all datasets within each scenario for each fitted model and where fitted models have assumed CS correlation structure.