Bin-CE: A comprehensive web application to decide upon the best set of outcomes to be combined in a binary composite endpoint

Abstract

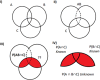
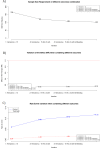
The estimation of the Sample Size Requirement (SSR) when using a binary composite endpoint (i.e. two or more outcomes combined in a unique primary endpoint) is not trivial. Besides information about the rate of events for each outcome, information about the strength of association between the outcomes is crucial, since it can determine an increase or decrease of the SSR. Specifically, the greater the strength of association between outcomes the higher the SSR. We present Bin-CE, a free tool to assist clinicians for computing the SSR for binary composite endpoints. In a first step, the user enters a set of candidate outcomes, the assumed rate of events for each outcome and the assumed effect of therapy on each outcome. Since the strength of the association between outcomes is usually unknown, a semi-parametric approach linking the a priori clinical knowledge of the potential degree of association between outcomes with the exact values of these parameters was programmed with Bin-CE. Bin-CE works with a recursive algorithm to choose the best combination of outcomes that minimizes the SSR. In addition, Bin-CE computes the sample size using different algorithms and shows different figures plotting the magnitude of the sample size reduction, and the effect of different combinations of outcomes on the rate of the primary endpoint. Finally, Bin-CE is programmed to perform sensitivity analyses. This manuscript presents the mathematic bases and introduces the reader to the use of Bin-CE using a real example.

Fig 1. Bin-CE workflow.

Fig 2. Data showed on screen 1: Rate of events and effect of the therapy.

On the first screen (Input Data), the user fixes the number of outcomes, the hypothesis contrast and the type I/II errors assumed. Then the user assigns the following parameters a) the label of each outcome, b) the rate of events in the control group, c) the effect of the therapy measured as a risk ratio and d) if any of the outcomes is considered as the RE.

Fig 3. Data showed on screen 2: Joint probability (second-order association).

On the second screen (Association) the known joint probabilities for the simultaneous occurrence of each pair of outcomes should be declared and their values uploaded in the appropriate cell. The semi-parametric approximations according to the Fréchet Bounds are employed for the unknown associations.

Fig 4. Data showed on Screen 3: Checking upload data and firsts results.

On the third screen (Data) the user can check the data uploaded (i.e. labels, the RE, the rate of events in the control groups, the effect of the therapy and a triangular-matrix with all the pairs of joint probabilities). On this screen the SSR for the RE or for the outcome with a minimum SSR is shown. Finally, Bin-CE depicts a plot with the range of SSR when combining the RE with each of the other AE assuming the lower and the higher association of the Fréchet Bounds.

Fig 5

Second and third-order associations between three hypothetical outcomes (A, B and C). The association between a new hypothetical CE obtained by combination of outcomes A and B and the outcome C (red-colored probability) is the result of combining the joint probability between the pairs of outcomes A and C and the outcomes B and C. The value of this probability is (1): Prob((X_AC = 1)∩(X_BC = 1)) = π_AC+π_BC−π_ABC≈π_AC+π_BC−π_AC*π_BC. Then Bin-CE estimates the unknown joint probability among the 3 outcomes π_ABC with the product of both probabilities (i.e. π_AC*π_BC). Although this is only an approximation, the potential error should be small since the real proportion of patients with the 3 outcomes has to be within the Fréchet Bounds (max{0;π_AC+π_BC−1}≤π_ABC≤min{π_AB,π_BC}).

Fig 6. Data showed on screen 4: Results (table).

Each line presents the CE selected in each step, specifically: the label of the combined components, the incidence rate and the Relative Risk, the SSR (number of subjects required in each treatment group) and the proportion of SSR compared to that used for the isolated RE.

Fig 7. Data showed on screen 4.

Plots of the main results. A Sample Size Requirement in each iteration. Y-axis is ranged from zero and it represents the SSR computed within each iteration. X-axis shows each one of the Bin-CE iterations. In the example, first iteration corresponds to the RE “Hematoma > 15 cm.”, with SSR of 166. The second iteration corresponds to the CE “Hematoma > 15 cm” and “Hb drop ≥3 g/dl with overt bleeding”, with a SSR of 121. Finally Bin-CE proposes to combine 4 outcomes to the last CE, in this case the SSR is of 102. B Effect of the therapy in each Bin-CE iteration. In the example, the effect of the therapy was a RR of 0.09 in the first iteration and it increased (decreased the efficacy) until 0.16 at the last iteration of Bin-CE. C Rate of events in each iteration. This plot presents, for each Bin-CE iteration, the rate of events for both the control group and the treatment group. In the example, the rate of event for the control and treatment group in the first iteration were 6% and 0.54% respectively, which increased to 9.48% and 1.33% in the second iteration. Finally, a small increase in rates was achieved through the third and fourth iteration, in agreement with the small reduction in SSR displayed in A.