All-photonic quantum teleportation using on-demand solid-state quantum emitters
- PMID: 30555916
- PMCID: PMC6294597
- DOI: 10.1126/sciadv.aau1255
All-photonic quantum teleportation using on-demand solid-state quantum emitters
Abstract
All-optical quantum teleportation lies at the heart of quantum communication science and technology. This quantum phenomenon is built up around the nonlocal properties of entangled states of light that, in the perspective of real-life applications, should be encoded on photon pairs generated on demand. Despite recent advances, however, the exploitation of deterministic quantum light sources in push-button quantum teleportation schemes remains a major open challenge. Here, we perform an important step toward this goal and show that photon pairs generated on demand by a GaAs quantum dot can be used to implement a teleportation protocol whose fidelity violates the classical limit (by more than 5 SDs) for arbitrary input states. Moreover, we develop a theoretical framework that matches the experimental observations and that defines the degree of entanglement and indistinguishability needed to overcome the classical limit independently of the input state. Our results emphasize that on-demand solid-state quantum emitters are one of the most promising candidates to realize deterministic quantum teleportation in practical quantum networks.
Figures

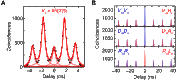
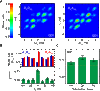
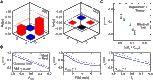
References
-
- Kimble H. J., The quantum internet. Nature 453, 1023–1030 (2008). - PubMed
-
- Lo H.-K., Chau H. F., Unconditional security of quantum key distribution over arbitrarily long distances. Science 283, 2050–2056 (1999). - PubMed
-
- Bennett C. H., Brassard G., Crépeau C., Jozsa R., Peres A., Wootters W. K., Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 70, 1895–1899 (1993). - PubMed
-
- Bouwmeester D., Pan J.-W., Mattle K., Eibl M., Weinfurter H., Zeilinger A., Experimental quantum teleportation. Nature 390, 575–579 (1997).
-
- Boschi D., Branca S., De Martini F., Hardy L., Popescu S., Experimental realization of teleporting an unknown pure quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 80, 1121–1125 (1998).
LinkOut - more resources
Full Text Sources

