Competing Mechanisms of Stress-Assisted Diffusivity and Stretch-Activated Currents in Cardiac Electromechanics

Abstract

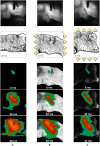
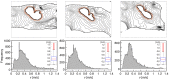
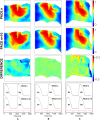
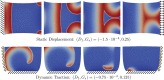
We numerically investigate the role of mechanical stress in modifying the conductivity properties of cardiac tissue, and also assess the impact of these effects in the solutions generated by computational models for cardiac electromechanics. We follow the recent theoretical framework from Cherubini et al. (2017), proposed in the context of general reaction-diffusion-mechanics systems emerging from multiphysics continuum mechanics and finite elasticity. In the present study, the adapted models are compared against preliminary experimental data of pig right ventricle fluorescence optical mapping. These data contribute to the characterization of the observed inhomogeneity and anisotropy properties that result from mechanical deformation. Our novel approach simultaneously incorporates two mechanisms for mechano-electric feedback (MEF): stretch-activated currents (SAC) and stress-assisted diffusion (SAD); and we also identify their influence into the nonlinear spatiotemporal dynamics. It is found that (i) only specific combinations of the two MEF effects allow proper conduction velocity measurement; (ii) expected heterogeneities and anisotropies are obtained via the novel stress-assisted diffusion mechanisms; (iii) spiral wave meandering and drifting is highly mediated by the applied mechanical loading. We provide an analysis of the intrinsic structure of the nonlinear coupling mechanisms using computational tests conducted with finite element methods. In particular, we compare static and dynamic deformation regimes in the onset of cardiac arrhythmias and address other potential biomedical applications.

Keywords: cardiac electromechanics; finite elasticity; reaction-diffusion; stress-assisted diffusion; stretch-activated currents.

Figure 1

MEF observed in pig right ventricle via fluorescence optical mapping. From top to bottom, we provide: underlying tissue structure in reference (A) and deformed (B,C) states; activation isochrones each 4ms originating from the stimulation point (red spot in the field of view–the bar indicates a length of 1cm), and activation sequences. The three cases refer to no-stretch (A), static horizontally (B), and vertical (C) stretch in the directions indicated by the yellow arrows. The sequence of spatial activation uses the color code scaled to the AP level (yellow/green–high/low). Selected frames highlight the anisotropy induced by stretch. The outer black region is the noisy area not useful for the field of view.

Figure 2

CV histograms measured on tissue wedges for three different loading states overlapping local measures for seven consecutive activations at constant pacing cycle length of 1s. All the normal directions to the AP propagation are considered as indicated by orange arrows on a representative isochrone contour. The box plot of the distribution is provided as inset for the three histogram, respectively, highlighting the amount of dispersion and the reduction of CV under stretch (see Table 1 for details). Cut-off of spurious values is set at 0.05 and 1.3 m/s.

Figure 3

Spatial and temporal comparison of ventricular activation at constant pacing cycle length of 1s under different mechanical loadings [free (A), horizontal (B) and vertical (C) stretch as in Figure 1]. The first two rows show the spatial distribution of the normalized voltage for beat n and beat n + 10 with the corresponding difference in the third row (color code is indicated). The last row indicates the time course of a representative pixel in the center of the field of view for two consecutive beats n and n + 10 with the corresponding difference provided in the red trace.

Figure 4

Example of structured mesh employed in the computational results. The grid is displayed on the deformed configuration when the domain is subject to traction (arrows) and fixed displacement (lines) boundary conditions, and a zoom exemplifies the mesh resolution for a rather coarse spiral front.

Figure 5

MEF parameter space associated to the conduction velocity measured on the propagating front of a planar excitation wave (stimulation on the left edge and propagation toward the right boundary) elicited on a static uniaxially stretched domain (CV in [m/s]). Four selected combinations of MEF parameters (A,B,C,D, in Table 3) are highlighted together with two additional cases in which CV was not recorded. On the right, three consecutive time frames of the activation are selected.

Figure 6

Point-wise activation frame for five different static boundary conditions qualitatively reproducing ventricle wedge preparation measurements considering the parameter combination $(D_1,G_s)=(-0.75·10^{-4},0)$: (A) free edges, (B) horizontal displacement, (C) vertical displacement, (D) horizontal traction, (E) vertical traction. Color code refers to the normalized action potential.

Figure 7

S1-S2 stimulation protocol applied on a static uniaxial stretched configuration for different combinations of MEF parameters (D₁, G_s) as provided in Table 3. The color code refers to normalized dimensionless membrane potential, u, (blue-red mapped to [0–1]). Selected time frames are provided in the subpanels.

Figure 8

Example of different propagation patterns according to different mechanical boundary conditions and parameter space. First row shows the uniaxial static displacement configuration for which the selected parameters induce additional activations from the corners of the domain due to the excessive level of SAC (G_s). Second row shows the dynamic traction configuration for which the initiated spiral wave goes through breakup due to the effect of mechanical loading.

Figure 9

Tip trajectories for four combinations of MEF parameters (D₁, G_s) (see Table 3), applying static/dynamic–displacement/traction boundary conditions as indicated in the corresponding inset. Inset color code refers to the magnitude of the displacement field. (A) The last second of simulation is shown for the four cases with localized cores. (B) The last 3 s of simulations are shown highlighting the differences of the meandering. (C) Different times are shown for the four cases since for G_s > 0 the spirals exit the domain soon after initiation. (D) The last 3 s are shown for the case G_s > 0 highlighting the different meandering obtained with respect to G_s = 0. Minor discontinuities are due to the frame resolution for post processing analysis and are not linked to the accuracy of the numerical solution.

Figure 10

(A) Clockwise (blue) and counterclockwise (red) tip trajectories obtained in a dynamic uniaxially stretched case with MEF parameters D₁ = 0, G_s = 0.125 and initiated via the S1-S2 stimulation protocol. (B) Counterclockwise spiral initiation from top (red) or bottom (blue) boundary. Side panels show progressive spiral frames for the two cases.