Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2018 Dec 20;13(12):e0208726.
doi: 10.1371/journal.pone.0208726. eCollection 2018.

A new mark-recapture approach for abundance estimation of social species

Jena R Hickey  1 , Rahel Sollmann  2
Affiliations

A new mark-recapture approach for abundance estimation of social species

Jena R Hickey et al. PLoS One. .

Abstract

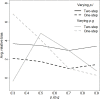
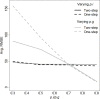
Accurate estimates of population abundance are a critical component of species conservation efforts in order to monitor the potential recovery of populations. Capture-mark-recapture (CMR) is a widely used approach to estimate population abundance, yet social species moving in groups violate the assumption of CMR approaches that all individuals in the population are detected independently. We developed a closed CMR model that addresses an important characteristic of group-living species-that individual-detection probability typically is conditional on group detection. Henceforth termed the Two-Step model, this approach first estimates group-detection probability and then-conditional on group detection-estimates individual-detection probability for individuals within detected groups. Overall abundance is estimated assuming that undetected groups have the same average group size as detected groups. We compared the performance of this Two-Step CMR model to a conventional (One-Step) closed CMR model that ignored group structure. We assessed model sensitivity to variation in both group- and individual-detection probability. Both models returned overall unbiased estimates of abundance, but the One-Step model returned deceptively narrow Bayesian confidence intervals (BCI) that failed to encompass the correct population abundance an average 52% of the time. Contrary, under the Two-Step model, CI coverage was on average 96%. Both models had similar root mean squared errors (RMSE), except for scenarios with low group detection probability, where the Two-Step model had much lower RMSE. For illustration with a real data set, we applied the Two-Step and regular model to non-invasive genetic capture-recapture data of mountain gorillas (Gorilla beringei beringei). As with simulations, abundance estimates under both models were similar, but the Two-Step model estimate had a wider confidence interval. Results support using the Two-Step model for species living in constant groups, particularly when group detection probability is low, to reduce risk of bias and adequately portray uncertainty in abundance estimates. Important sources of variation in detection need to be incorporated into the Two-Step model when applying it to field data.

PubMed Disclaimer

Conflict of interest statement

The authors have declared that no competing interests exist.

Figures

Fig 1
Fig 1. Average relative bias of the posterior mean of abundance (N^) from the Two-Step and the One-Step CMR model over a range of group-detection probabilities (pg) and individual-detection probability (pi).
When pg was varied, pi was held constant at 0.7, and vice versa.
Fig 2
Fig 2. 95% Bayesian Credible Interval (BCI) coverage for abundance estimates across 1000 simulated populations for the Two-Step and the One-Step CMR model over a range of group-detection probabilities (pg) and individual-detection probability (pi).
When pg was varied, pi was held constant at 0.7, and vice versa.
Fig 3
Fig 3. Root mean square error (RMSE) for abundance estimates across 1000 simulated populations for the Two-Step and the One-Step CMR model over a range of group-detection probabilities (pg) and individual-detection probability (pi).
When pg was varied, pi was held constant at 0.7, and vice versa.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

References

    1. Pollock K. Building Models of Capture-Recapture Experiments. J of the Royal Statistical Society, Series D (The Statistician). 1976; 25(4): 253–259. 10.2307/2988083 - DOI
    1. Otis D, Burnham K, White G, Anderson D. Statistical Inference from Capture Data on Closed Animal Populations. Wildlife Monogr. 1978; 62: 3–135. Retrieved from http://www.jstor.org/stable/3830650
    1. Begon M. Abuses of mathematical techniques in ecology: applications of Jolly’s capture–recapture method. Oikos. 1983; 40:155–158.
    1. Eggert LS, Eggert JA, Woodruff DS. Estimating population sizes for elusive animals: the forest elephants of Kakum National Park, Ghana. Molecular Ecol. 2003; 12(6): 1389–1402. - PubMed
    1. Cam E. Contribution of capture-mark-recapture modeling to studies of evolution by natural selection. In: Thomson DL, et al., editors. Modeling demographic processes in marked populations. Environmental and Ecological Statistics, 3: Springer; 2009. p. 83–129. 10.1007/978-0-387-78151-8 5, - DOI

Publication types