Spin locking in liquid entrapped in nanocavities: Application to study connective tissues
- PMID: 30580046
- PMCID: PMC6942517
- DOI: 10.1016/j.jmr.2018.12.012
Spin locking in liquid entrapped in nanocavities: Application to study connective tissues
Abstract
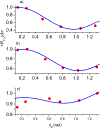
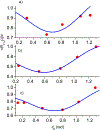
Study of the spin-lattice relaxation in the spin-locking state offers important information about atomic and molecular motions, which cannot be obtained by spin lattice relaxation in strong external magnetic fields. The application of this technique for the investigation of the spin-lattice relaxation in biological samples with fibril structures reveals an anisotropy effect for the relaxation time under spin locking, T1ρ. To explain the anisotropy of the spin-lattice relaxation under spin-locking in connective tissue a model which represents a tissue by a set of nanocavities containing water is used. The developed model allows us to estimate the correlation time for water molecular motion in articular cartilage, τc=30μs and the averaged nanocavity volume, V≃5400nm3. Based on the developed model which represents a connective tissue by a set of nanocavities containing water, a good agreement with the experimental data from an articular cartilage and a tendon was demonstrated. The fitting parameters were obtained for each layer in each region of the articular cartilage. These parameters vary with the known anatomic microstructures of the tissue. Through Gaussian distributions to nanocavity directions, we have calculated the anisotropy of the relaxation time under spin locking T1ρ for a human Achilles tendon specimen and an articular cartilage. The value of the fitting parameters obtained at matching of calculation to experimental results can be used in future investigations for characterizing the fine fibril structure of biological samples.
Keywords: Anisotropy; Cartilage; Nanocavity; Spin lattice relaxation time T(1)(ρ); Spin locking.
Copyright © 2018 Elsevier Inc. All rights reserved.
Conflict of interest statement
Figures



Similar articles
-
Anisotropy of Transverse Spin Relaxation in H2O-D2O Liquid Entrapped in Nanocavities: Application to Studies of Connective Tissues.Hyperfine Interact. 2021 Dec;242(1):19. doi: 10.1007/s10751-021-01731-9. Epub 2021 Oct 30. Hyperfine Interact. 2021. PMID: 35990926 Free PMC article.
-
Dynamics of Zeeman and dipolar states in the spin locking in a liquid entrapped in nano-cavities: Application to study of biological systems.J Magn Reson. 2021 Apr;325:106933. doi: 10.1016/j.jmr.2021.106933. Epub 2021 Feb 11. J Magn Reson. 2021. PMID: 33636633 Free PMC article.
-
Spin-lattice relaxation in liquid entrapped in a nanocavity.J Magn Reson. 2020 Feb;311:106669. doi: 10.1016/j.jmr.2019.106669. Epub 2019 Dec 16. J Magn Reson. 2020. PMID: 31881481 Free PMC article.
-
Anisotropy of spin-spin and spin-lattice relaxation times in liquids entrapped in nanocavities: Application to MRI study of biological systems.J Magn Reson. 2016 Feb;263:71-78. doi: 10.1016/j.jmr.2015.12.015. Epub 2016 Jan 4. J Magn Reson. 2016. PMID: 26773529
-
Multiquantum filters and order in tissues.NMR Biomed. 2001 Apr;14(2):112-32. doi: 10.1002/nbm.687. NMR Biomed. 2001. PMID: 11320537 Review.
Cited by
-
Anisotropy of transverse and longitudinal relaxations in liquids entrapped in nano- and micro-cavities of a plant stem.J Magn Reson. 2021 Oct;331:107051. doi: 10.1016/j.jmr.2021.107051. Epub 2021 Aug 18. J Magn Reson. 2021. PMID: 34455368 Free PMC article.
-
Study of the collagen tissue nanostructure by analyzing the echo decay obtained using the MRI technique.Soft Matter. 2024 May 29;20(21):4282-4290. doi: 10.1039/d4sm00312h. Soft Matter. 2024. PMID: 38757720 Free PMC article.
-
Anisotropy of Transverse Spin Relaxation in H2O-D2O Liquid Entrapped in Nanocavities: Application to Studies of Connective Tissues.Hyperfine Interact. 2021 Dec;242(1):19. doi: 10.1007/s10751-021-01731-9. Epub 2021 Oct 30. Hyperfine Interact. 2021. PMID: 35990926 Free PMC article.
-
Dynamics of Zeeman and dipolar states in the spin locking in a liquid entrapped in nano-cavities: Application to study of biological systems.J Magn Reson. 2021 Apr;325:106933. doi: 10.1016/j.jmr.2021.106933. Epub 2021 Feb 11. J Magn Reson. 2021. PMID: 33636633 Free PMC article.
-
Spin-lattice relaxation in liquid entrapped in a nanocavity.J Magn Reson. 2020 Feb;311:106669. doi: 10.1016/j.jmr.2019.106669. Epub 2019 Dec 16. J Magn Reson. 2020. PMID: 31881481 Free PMC article.
References
-
- Abraham A (1961) The principles of nuclear magnetism. Oxford Clarendon Press.
-
- Callaghan PT (1991) Principles of nuclear magnetic resonance microscopy. Oxford Clarendon Press.
-
- Haeberlen U and Waugh JS (1969) Spin-lattice relaxation in periodically perturbed systems. Phys Rev 185:420.
-
- Mehring M (1978) High resolution NMR spectroscopy in solids. Springer-Verlag.
-
- Haeberlen U (1978) High resolution NMR in solids. Academic Press.
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources

