Comparative performance of the finite element method and the boundary element fast multipole method for problems mimicking transcranial magnetic stimulation (TMS)

Abstract

Objective: A study pertinent to the numerical modeling of cortical neurostimulation is conducted in an effort to compare the performance of the finite element method (FEM) and an original formulation of the boundary element fast multipole method (BEM-FMM) at matched computational performance metrics.

Approach: We consider two problems: (i) a canonic multi-sphere geometry and an external magnetic-dipole excitation where the analytical solution is available and; (ii) a problem with realistic head models excited by a realistic coil geometry. In the first case, the FEM algorithm tested is a fast open-source getDP solver running within the SimNIBS 2.1.1 environment. In the second case, a high-end commercial FEM software package ANSYS Maxwell 3D is used. The BEM-FMM method runs in the MATLAB^® 2018a environment.

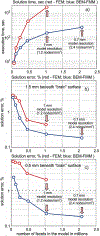
Main results: In the first case, we observe that the BEM-FMM algorithm gives a smaller solution error for all mesh resolutions and runs significantly faster for high-resolution meshes when the number of triangular facets exceeds approximately 0.25 M. We present other relevant simulation results such as volumetric mesh generation times for the FEM, time necessary to compute the potential integrals for the BEM-FMM, and solution performance metrics for different hardware/operating system combinations. In the second case, we observe an excellent agreement for electric field distribution across different cranium compartments and, at the same time, a speed improvement of three orders of magnitude when the BEM-FMM algorithm used.

Significance: This study may provide a justification for anticipated use of the BEM-FMM algorithm for high-resolution realistic transcranial magnetic stimulation scenarios.

Figure 1

Boundary between two conducting compartments with different conductivities and surface charge density ρ (r) residing at the boundary.

Figure 2

(a) Model geometry; (b) surface mesh topology for sphere #2 with the mesh resolution of 2.9 mm and the mesh density of 0.14 nodes mm⁻².

Figure 3

(a) Solid-conductor coil model in ANSYS FEM software and; (b) wire-conductor coil model in BEM-FMM software.

Figure 4

(a) Solution time; (b) solution error of the FEM and BEM-FMM algorithms, respectively, both as functions of the number of facets in the model (model resolution and/or mesh density) at 1.5 mm beneath the ‘brain’ surface; (c) the same result at 0.5 mm beneath the ‘brain’ surface.

Figure 5

(a) and (b) Computation geometry, position of the observation line, and surface field distributions for head #101309 given 5 kA of coil current at 3 kHz; (c) electric field comparison along the line. BEM-FMM solution is shown by solid curves; the ANSYS Maxwell 3D FEM solution is given by dotted curves.