Data-Augmented Modeling of Intracranial Pressure
- PMID: 30607645
- PMCID: PMC7155952
- DOI: 10.1007/s10439-018-02191-z
Data-Augmented Modeling of Intracranial Pressure
Abstract
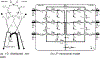
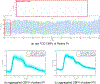
Precise management of patients with cerebral diseases often requires intracranial pressure (ICP) monitoring, which is highly invasive and requires a specialized ICU setting. The ability to noninvasively estimate ICP is highly compelling as an alternative to, or screening for, invasive ICP measurement. Most existing approaches for noninvasive ICP estimation aim to build a regression function that maps noninvasive measurements to an ICP estimate using statistical learning techniques. These data-based approaches have met limited success, likely because the amount of training data needed is onerous for this complex applications. In this work, we discuss an alternative strategy that aims to better utilize noninvasive measurement data by leveraging mechanistic understanding of physiology. Specifically, we developed a Bayesian framework that combines a multiscale model of intracranial physiology with noninvasive measurements of cerebral blood flow using transcranial Doppler. Virtual experiments with synthetic data are conducted to verify and analyze the proposed framework. A preliminary clinical application study on two patients is also performed in which we demonstrate the ability of this method to improve ICP prediction.
Keywords: Cerebrovascular dynamics; Data assimilation; Patient-specific modeling; Transcranial Doppler.
Figures
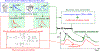



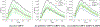

Similar articles
-
Regression-based noninvasive estimation of intracranial pressure.Annu Int Conf IEEE Eng Med Biol Soc. 2017 Jul;2017:4001-4004. doi: 10.1109/EMBC.2017.8037733. Annu Int Conf IEEE Eng Med Biol Soc. 2017. PMID: 29060774
-
A Deep Learning Framework for Deriving Noninvasive Intracranial Pressure Waveforms from Transcranial Doppler.Ann Neurol. 2023 Jul;94(1):196-202. doi: 10.1002/ana.26682. Epub 2023 Jun 1. Ann Neurol. 2023. PMID: 37189299 Free PMC article.
-
Noninvasive Intracranial Pressure Determination in Patients with Subarachnoid Hemorrhage.Acta Neurochir Suppl. 2016;122:65-8. doi: 10.1007/978-3-319-22533-3_13. Acta Neurochir Suppl. 2016. PMID: 27165879
-
Measuring elevated intracranial pressure through noninvasive methods: a review of the literature.J Neurosurg Anesthesiol. 2013 Oct;25(4):372-85. doi: 10.1097/ANA.0b013e31829795ce. J Neurosurg Anesthesiol. 2013. PMID: 23715045 Review.
-
Clinical applications of a non-invasive ICP monitoring method.Eur J Ultrasound. 2002 Nov;16(1-2):37-45. doi: 10.1016/s0929-8266(02)00044-7. Eur J Ultrasound. 2002. PMID: 12470849 Review.
Cited by
-
Reducing Geometric Uncertainty in Computational Hemodynamics by Deep Learning-Assisted Parallel-Chain MCMC.J Biomech Eng. 2022 Dec 1;144(12):121009. doi: 10.1115/1.4055809. J Biomech Eng. 2022. PMID: 36166284 Free PMC article.
-
Identification of Pulse Onset on Cerebral Blood Flow Velocity Waveforms: A Comparative Study.Biomed Res Int. 2019 Jul 2;2019:3252178. doi: 10.1155/2019/3252178. eCollection 2019. Biomed Res Int. 2019. PMID: 31355255 Free PMC article. Review.
-
Clinical Decision Support for Traumatic Brain Injury: Identifying a Framework for Practical Model-Based Intracranial Pressure Estimation at Multihour Timescales.JMIR Med Inform. 2021 Mar 22;9(3):e23215. doi: 10.2196/23215. JMIR Med Inform. 2021. PMID: 33749613 Free PMC article.
-
Review: pathophysiology of intracranial hypertension and noninvasive intracranial pressure monitoring.Fluids Barriers CNS. 2020 Jun 23;17(1):40. doi: 10.1186/s12987-020-00201-8. Fluids Barriers CNS. 2020. PMID: 32576216 Free PMC article. Review.
-
A computational bio-chemo-mechanical model of in vivo tissue-engineered vascular graft development.Integr Biol (Camb). 2020 Apr 14;12(3):47-63. doi: 10.1093/intbio/zyaa004. Integr Biol (Camb). 2020. PMID: 32222759 Free PMC article.
References
-
- Andrews PJ, Citerio G, Longhi L, Polderman K, Sahuquillo J, Vajkoczy P, Care N-I, E. M. N. S. of the European Society of Intensive Care Medicine et al. NICEM consensus on neurological monitoring in acute neurological disease. Intensive care medicine 34:1362–1370, 2008. - PubMed
-
- Asiedu DP, Lee K-J, Mills G, and Kaufmann EE. A review of non-invasive methods of monitoring intracranial pressure. Journal of Neurology Research 4:1–6, 2014.
-
- Bertoglio C, Moireau P, and Gerbeau J-F. Sequential parameter estimation for fluid–structure problems: Application to hemodynamics. International Journal for Numerical Methods in Biomedical Engineering 28:434–455, 2012. - PubMed
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Miscellaneous

