A Metric for Evaluating Neural Input Representation in Supervised Learning Networks
- PMID: 30618549
- PMCID: PMC6302114
- DOI: 10.3389/fnins.2018.00913
A Metric for Evaluating Neural Input Representation in Supervised Learning Networks
Abstract
Supervised learning has long been attributed to several feed-forward neural circuits within the brain, with particular attention being paid to the cerebellar granular layer. The focus of this study is to evaluate the input activity representation of these feed-forward neural networks. The activity of cerebellar granule cells is conveyed by parallel fibers and translated into Purkinje cell activity, which constitutes the sole output of the cerebellar cortex. The learning process at this parallel-fiber-to-Purkinje-cell connection makes each Purkinje cell sensitive to a set of specific cerebellar states, which are roughly determined by the granule-cell activity during a certain time window. A Purkinje cell becomes sensitive to each neural input state and, consequently, the network operates as a function able to generate a desired output for each provided input by means of supervised learning. However, not all sets of Purkinje cell responses can be assigned to any set of input states due to the network's own limitations (inherent to the network neurobiological substrate), that is, not all input-output mapping can be learned. A key limiting factor is the representation of the input states through granule-cell activity. The quality of this representation (e.g., in terms of heterogeneity) will determine the capacity of the network to learn a varied set of outputs. Assessing the quality of this representation is interesting when developing and studying models of these networks to identify those neuron or network characteristics that enhance this representation. In this study we present an algorithm for evaluating quantitatively the level of compatibility/interference amongst a set of given cerebellar states according to their representation (granule-cell activation patterns) without the need for actually conducting simulations and network training. The algorithm input consists of a real-number matrix that codifies the activity level of every considered granule-cell in each state. The capability of this representation to generate a varied set of outputs is evaluated geometrically, thus resulting in a real number that assesses the goodness of the representation.
Keywords: cerebellum; convex geometry; granular layer; high dimensionality; inferior colliculus; non-negativity constraints; population coding; supervised learning.
Figures



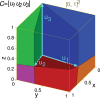

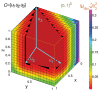
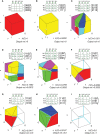

References
-
- Albus J. S. (1971). The theory of cerebellar function. Math. Biosci. 10, 25–61. 10.1016/0025-5564(71)90051-4 - DOI
-
- Albus J. S. (1975). A new approach to manipulator control: The cerebellar model articulation controller (CMAC). J. Dyn. Syst. Measure. Control 97, 220–227. 10.1115/1.3426922 - DOI
-
- Arfken G. (1985). Gram-Schmidt Orthogonalization, Mathematical Methods for Physicists, 3rd Edn. Orlando, FL: Academic; Press, 516–520.
-
- Avis D. (1980). On the extreme rays of the metric cone. Can. J. Math. 32, 126–144. 10.4153/CJM-1980-010-0 - DOI
LinkOut - more resources
Full Text Sources

