Morphology of Evaporating Sessile Microdroplets on Lyophilic Elliptical Patches

Abstract

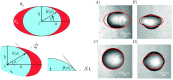
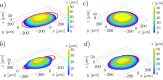
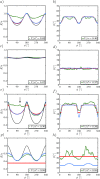
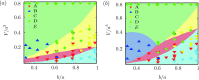
The evaporation of droplets occurs in a large variety of natural and technological processes such as medical diagnostics, agriculture, food industry, printing, and catalytic reactions. We study the different droplet morphologies adopted by an evaporating droplet on a surface with an elliptical patch with a different contact angle. We perform experiments to observe these morphologies and use numerical calculations to predict the effects of the patched surfaces. We observe that tuning the geometry of the patches offers control over the shape of the droplet. In the experiments, the drops of various volumes are placed on elliptical chemical patches of different aspect ratios and imaged in 3D using laser scanning confocal microscopy, extracting the droplet's shape. In the corresponding numerical simulations, we minimize the interfacial free energy of the droplet, by employing Surface Evolver. The numerical results are in good qualitative agreement with our experimental data and can be used for the design of micropatterned structures, potentially suggesting or excluding certain morphologies for particular applications. However, the experimental results show the effects of pinning and contact angle hysteresis, which are obviously absent in the numerical energy minimization. The work culminates with a morphology diagram in the aspect ratio vs relative volume parameter space, comparing the predictions with the measurements.

Figure 1

Scheme of the morphologies of a droplet as seen from the top as expected from the calculations by Dević et al.

Figure 2

Left: Coordinate system employed in this paper. θ₁ and θ₂ are, respectively, the Young’s angles of the lyophobic (white) and lyophilic (red) regions. R(ϕ) is the distance from the center of the ellipse to the contact line of the droplet (blue), and a and b are the major and minor axis, respectively. S indicates the vertical section. Right: Experimental results. Top view images were taken during the evaporation of various droplets on ellipses with different sizes and aspect ratios; the red contours represent the elliptical patches on the surface. (A) Morphology A, droplet on an ellipse of aspect ratio b/a = 0.61 and semimajor axis a = 512 ± 16 μm. (B) Morphology B, droplet on an ellipse of aspect ratio b/a = 0.43 and semimajor axis a = 392 ± 20 μm. (C) Morphology C, droplet on an ellipse of aspect ratio b/a = 0.98 and semimajor axis a = 410 ± 20 μm. (D) Morphology D, droplet on an ellipse of aspect ratio b/a = 0.69 and semimajor axis a = 411 ± 20 μm.

Figure 3

(a) Array of ellipses of aspect ratios varying from 0.3 to 1 and sizes varying from a = 320 μm to b = 2500 μm fabricated on the photomask. (b) Simplified steps of the substrates’ fabrication in the order indicated by the numbers.

Figure 4

Three-dimensional reconstruction of the shape extracted from the LSCM data collected for four different droplets adopting morphologies A, B, C, and D, respectively, as performed for the extraction of the contact angle along the contact line with the shape of the elliptical patch, highlighted in red lines. Repeatability is subjected to the initial position of the droplet and pinning of the contact line which can affect the symmetry of the shape as well as delay the transition between phases as compared to the predictions. In Figure 6, all the morphologies observed during the experiments are shown.

Figure 5

Normalized footprint radius R/a and contact angle θ along the azimuthal coordinate ϕ (as defined in Figure 2). Experimental results for the four different morphologies (green). From top to bottom: morphology D (V/a³ = 0.40, b/a = 0.69, and a = 411 ± 20 μm); morphology C (V/a³ = 0.37, b/a = 0.98, and a = 410 ± 20 μm); morphology B (V/a³ = 0.30, b/a = 0.43, and a = 392 ± 20 μm); and morphology A (V/a³ = 0.08, b/a = 0.61, and a = 512 ± 16 μm). Results of the numerical simulations considering the lyophilic contact angles θ₂ = 15° (blue) and θ₂ = 33° (red). The black curve in the radius plot shows the contour of the elliptical patch.

Figure 6

Morphology diagrams in aspect ratio b/a vs relative volume V/a³ phase space showing the morphologies A, B, C, D, and E. (a) Experimental results displayed together with the computational results considering θ₁= 49° and θ₂ = θ_r2 = 15° (b) Experimental results displayed with the computational results considering θ₁= 49° and θ₂ = θ_a2 = 33°. The main features for A–D are indicated in Figure 4, while E shows the case in which the droplet is small enough to adopt the trivial spherical cap shape inside the patch. The color shadowed regions represent the morphologies obtained with our calculations. Green, yellow, dark blue, red, and light blue regions represent, respectively, the regions where morphologies D, C, B, A, and E were found in our calculations, and the colored markers show the experimental points specified in the legend.