Precision ultrasound sensing on a chip

Abstract

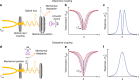
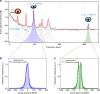
Ultrasound sensors have wide applications across science and technology. However, improved sensitivity is required for both miniaturisation and increased spatial resolution. Here, we introduce cavity optomechanical ultrasound sensing, where dual optical and mechanical resonances enhance the ultrasound signal. We achieve noise equivalent pressures of 8-300 μPa Hz^-1/2 at kilohertz to megahertz frequencies in a microscale silicon-chip-based sensor with >120 dB dynamic range. The sensitivity far exceeds similar sensors that use an optical resonance alone and, normalised to the sensing area, surpasses previous air-coupled ultrasound sensors by several orders of magnitude. The noise floor is dominated by collisions from molecules in the gas within which the acoustic wave propagates. This approach to acoustic sensing could find applications ranging from biomedical diagnostics, to autonomous navigation, trace gas sensing, and scientific exploration of the metabolism-induced-vibrations of single cells.

Fig. 1

Principles of dispersive and dissipative cavity optomechanical acoustic sensing. a, d Conceptual schematics of Fabry–Pérot cavity-based dispersive (a) and dissipative (d) sensors. In a an applied acoustic force drives harmonic oscillation of a movable cavity end-mirror modulating the length and resonance frequency of the cavity. In d the force drives a mechanical element that modulates the decay rate of the cavity. The modulation is monitored via the change in optical transmission (T_opt) from the cavity. b, e Cavity transmission in the presence of dispersive and dissipative coupling, respectively. The solid blue curves show the cavity transmission for the initial position of the mechanical element while the red dashed curves show the modified cavity transmission due to displacement of the mechanical element. c, f Amplitude of external-force driven modulation in transmission (ΔT_opt) of the cavity optomechanical system for dispersive and dissipative coupling, respectively, versus the detuning Δ of the input laser field from the cavity resonance

Fig. 2

Device architecture and experimental schematic. a Scanning electron micrograph of a similar microdisk to that used in this study. The microdisk is an optical cavity which is evanescently coupled to a tapered optical fibre. The scale bar corresponds to 20 μm. b Finite-element simulations of the modeshapes of two typical mechanical modes of the microdisk (left: second-order flapping mode, right: crown mode). c The phase sensitive and thermally stabilised experimental setup used to characterise the sensor. NP nanopositioner, MD microdisk, PD photodetector, FPC fibre polarization controller, VOA variable optical attenuator, OI optical isolator, FG function generator, OSC digital oscilloscope, NA network analyser, SA spectrum analyser. d The simulated pressure participation ratio, i.e., the fraction of the total acoustic pressure acting on the mechanical structure, for a number of frequencies. The insets display the pressure distribution at 105, 281 and 421 kHz, respectively; while p/p_max is the ratio of the pressure to the pressure at the antinodes of the acoustic wave

Fig. 3

Noise spectrum and coupling mechanisms. a The noise spectral density of the microdisk coupled to the tapered fibre in the absence of acoustic signal. The blue dashed line specifies the shot noise level given by the laser intensity, and the black dashed line corresponds to the 1/f noise. The shaded Lorentzian peaks specify the combined noise due to intrinsic damping and gas damping for several mechanical modes of the device. The green and blue shading highlights examples of dispersively and dissipatively coupled mechanical modes, respectively. γ_m quantifies the total mechanical dissipation rate of each of these modes, including both gas and intrinsic damping. b, c The ultrasonic response as a function of laser-cavity detuning at frequencies of 98 and 315 kHz, resonant with the second-order crown and flapping modes of the disk, respectively. The shaded areas are fits based upon the theoretical expectation for system response as function of detuning (see Supplementary Fig. 1) corresponding to dissipative (b) and dispersive (c) coupling, respectively

Fig. 4

Evaluation of the noise equivalent pressure sensitivity and the linear dynamic range. a Noise spectral density of the sensor near a mechanical mode of the microdisk measured at an electrical bandwidth of 200 Hz. An ultrasonic pressure of 120 mPa at frequency of 318 kHz is applied to the device resulting in a signal-to-noise ratio of ~40 dB. The shot noise is shown with the dashed blue line. The thermomechanical noise introduced by intrinsic and gas damping is shown, respectively, by the purple and green shaded Lorenztian’s. The total noise is fitted with the black dash-dot line, in good agreement with theory, and is dominated by gas damping noise between 306 and 325 kHz. b Ultrasonic response of the sensor at different frequencies as a function of ultrasonic pressure. The dashed grey line is a guide to the eye indicating the expected slope for a linear response. The linear dynamic range (LDR) is >120 dB for a measurement integration time of 1 s, with its upper limit dictated by the measurement setup rather than the acoustic response. The solid lines correspond to the measured data for each frequency and the dashed lines connect these to the noise equivalent pressure that sets the lower limit of the LDR

Fig. 5

Ultrasonic force sensitivity in comparison with other air-coupled sensors. Ultrasonic force sensitivity is evaluated as the noise equivalent pressure sensitivity multiplied by the sensing area and plotted versus frequency: open circles correspond to this work and solid symbols show results of other optical (blue circles) and electrical (red squares) approaches. The improvement of the sensitivity in this work is especially notable between 80 kHz and 1 MHz. Citations to previous work are provided in the Supplementary Fig. 8