STRFs in primary auditory cortex emerge from masking-based statistics of natural sounds

Abstract

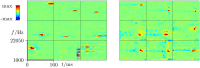
We investigate how the neural processing in auditory cortex is shaped by the statistics of natural sounds. Hypothesising that auditory cortex (A1) represents the structural primitives out of which sounds are composed, we employ a statistical model to extract such components. The input to the model are cochleagrams which approximate the non-linear transformations a sound undergoes from the outer ear, through the cochlea to the auditory nerve. Cochleagram components do not superimpose linearly, but rather according to a rule which can be approximated using the max function. This is a consequence of the compression inherent in the cochleagram and the sparsity of natural sounds. Furthermore, cochleagrams do not have negative values. Cochleagrams are therefore not matched well by the assumptions of standard linear approaches such as sparse coding or ICA. We therefore consider a new encoding approach for natural sounds, which combines a model of early auditory processing with maximal causes analysis (MCA), a sparse coding model which captures both the non-linear combination rule and non-negativity of the data. An efficient truncated EM algorithm is used to fit the MCA model to cochleagram data. We characterize the generative fields (GFs) inferred by MCA with respect to in vivo neural responses in A1 by applying reverse correlation to estimate spectro-temporal receptive fields (STRFs) implied by the learned GFs. Despite the GFs being non-negative, the STRF estimates are found to contain both positive and negative subfields, where the negative subfields can be attributed to explaining away effects as captured by the applied inference method. A direct comparison with ferret A1 shows many similar forms, and the spectral and temporal modulation tuning of both ferret and model STRFs show similar ranges over the population. In summary, our model represents an alternative to linear approaches for biological auditory encoding while it captures salient data properties and links inhibitory subfields to explaining away effects.

Fig 1. Illustration of the log-max approximation.

The figure shows the generation of cochleagrams according to the used preprocessing model and the different combination models (sum and max). First the cochleagrams generated from two different waveforms are shown (middle column, top and middle) as well as the cochleagram generated from the linear mixture of the two waveforms (bottom). On the right at the top, a cochleagram resulting from a linear mixture of the two individual cochleagrams is shown. On the right at the bottom, a cochleagram resulting from a point-wise maximum is shown. The non-linear maximum is much more closely aligned with the cochleagram of the actual mixed waveforms (dotted arrow).

Fig 2

A-C: Generative fields learned from the spectrograms of the natural sound data. A-B: The vertical axis of the fields are gammatone frequencies with lowest frequency band at the bottom and the horizontal axis spans over 160 ms from left to right. Each generative field is displayed as a 32 × 15 matrix. Fields in panels A-B were randomly selected. C: Every 5^th of the 500 most-frequently used fields is shown (ordered w.r.t. their marginal posterior probability from left to right and top to bottom). In total H = 1000 fields were learned. D: STRF estimates corresponding to the generative fields shown in panel C. A larger number of most-frequently employed fields can be found in the supplement, S1 Fig.

Fig 3. Example receptive fields from the model (left), and similar receptive fields as recorded in ferret A1 (right).

The times axis is the x-axis and is from -160 to 0 ms (left) and respectively -125 to 0 ms (right). The frequency axis is the y-axis and is from 1000-22050 Hz (left) and respectively 381-35618 Hz (right), in both cases with lowest frequency at the bottom.

Fig 4

A: Histogram of best spectral and temporal modulation frequencies for 241 experimentally recorded STRFs (left) and 241 model receptive fields for the MCA and BSC model (middle and right, respectively). 3/244 recorded STRFs were excluded (see Methods) as they had an L2 norm of zero. Yellow—high density, blue—low density. Histograms are scaled individually to fill the color scale (max is 104 fields for the experimental data, 67 fields for the MCA Model, and 46 fields for the BSC Model). B: Histogram shown for a wider range of scales and computed with a bin size of 8 instead of 12 Hz (as used in A). Histograms are scaled individually to fill the color scale (max is 78 fields for the experimental data, 36 fields for the MCA Model, and 35 fields for the BSC Model). C: For the histograms in B a dissimilarity measurement between data and MCA as well as between data and BSC was performed using χ² statistics as described in [44].

Fig 5

A: Distribution over neurons of temporal tuning widths of excitatory fields of the real (pink) and MCA model (grey) neurons. B: Distribution of temporal tuning widths of inhibitory fields. C: Distribution of frequency tuning widths of excitatory fields. D: Distribution of frequency tuning widths of inhibitory fields. For an illustration on how the tuning widths are computed see Supplementary S4 Fig.

Fig 6. Illustration of the emergence of inhibitory subfields.

A: Feedforward mapping from an input $\overrightarrow{y}$ to two neural units s₁ and s₂. The mapping is defined by two receptive fields with only positive entries. In this case, any strong activation of unit s₂ does not negatively effect unit s₁. For overlapping positive subfields, a stronger activation of s₂ will even result in a stronger activation of s₁ as well. B: Activations of neural units s₁ and s₂ according to a statistical model with non-negative generative fields (GFs). Both units compete to explain a presented input $\overrightarrow{y}$. A high probability for s₂ decreases the probability of s₁ and vica versa. This effect is known as “explaining away”, and it depends on the assumed model including the model for the combination of primitives, noise model, and prior. C: Illustration of an optimal feedforward mapping to approximate neural responses according to the statistical model in B. The stronger mutual suppression caused by explaining away is approximated by the introduction of inhibitory subfields. If the input is, e.g., now made stronger or less diffuse, then unit s₂ can increase while unit s₁ can simultaneously decrease, which is in accordance with probabilistic inference for a statistical model. D: Example of STRFs estimated from artificial data. The top row shows non-negative GFs. If the corresponding STRFs are now estimated using Eq 10, then negative subfields emerge (bottom row). For fields which do compete little with other fields (e.g., field three) the effect is the weakest. The strongest effects are observed for fields with large overlap (e.g. fields four and six). In general, explaining away effects increase with overcompleteness, i.e., with the number of GFs compared to input size. Color scales for all subfigures as in Fig 2A.