Adaptive, locally linear models of complex dynamics
- PMID: 30655347
- PMCID: PMC6358715
- DOI: 10.1073/pnas.1813476116
Adaptive, locally linear models of complex dynamics
Abstract
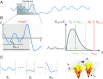
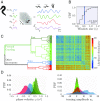
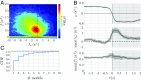
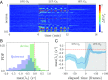
The dynamics of complex systems generally include high-dimensional, nonstationary, and nonlinear behavior, all of which pose fundamental challenges to quantitative understanding. To address these difficulties, we detail an approach based on local linear models within windows determined adaptively from data. While the dynamics within each window are simple, consisting of exponential decay, growth, and oscillations, the collection of local parameters across all windows provides a principled characterization of the full time series. To explore the resulting model space, we develop a likelihood-based hierarchical clustering, and we examine the eigenvalues of the linear dynamics. We demonstrate our analysis with the Lorenz system undergoing stable spiral dynamics and in the standard chaotic regime. Applied to the posture dynamics of the nematode Caenorhabditis elegans, our approach identifies fine-grained behavioral states and model dynamics which fluctuate about an instability boundary, and we detail a bifurcation in a transition from forward to backward crawling. We analyze whole-brain imaging in C. elegans and show that global brain dynamics is damped away from the instability boundary by a decrease in oxygen concentration. We provide additional evidence for such near-critical dynamics from the analysis of electrocorticography in monkey and the imaging of a neural population from mouse visual cortex at single-cell resolution.
Keywords: animal behavior; clustering; dynamical criticality; neural dynamics; time-series segmentation.
Copyright © 2019 the Author(s). Published by PNAS.
Figures

References
-
- Arratia PE, Voth GA, Gollub JP. Stretching and mixing of non-Newtonian fluids in time-periodic flows. Phys Fluids. 2005;17:1–10.
-
- Alakent B, Doruker P, Çamurdan MC. Time series analysis of collective motions in proteins. J Chem Phys. 2004;120:1072–1088. - PubMed
-
- Li K, Javer A, Keaveny EE, Brown AE. 2017. Recurrent neural networks with interpretable cells predict and classify worm behaviour. bioRxiv:10.1101/222208. Preprint, posted November 20, 2017.
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources

