Snap-jaw morphology is specialized for high-speed power amplification in the Dracula ant, Mystrium camillae

Abstract

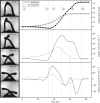
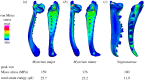
What is the limit of animal speed and what mechanisms produce the fastest movements? More than natural history trivia, the answer provides key insight into the form-function relationship of musculoskeletal movement and can determine the outcome of predator-prey interactions. The fastest known animal movements belong to arthropods, including trap-jaw ants, mantis shrimp and froghoppers, that have incorporated latches and springs into their appendage systems to overcome the limits of muscle power. In contrast to these examples of power amplification, where separate structures act as latch and spring to accelerate an appendage, some animals use a 'snap-jaw' mechanism that incorporates the latch and spring on the accelerating appendage itself. We examined the kinematics and functional morphology of the Dracula ant, Mystrium camillae, who use a snap-jaw mechanism to quickly slide their mandibles across each other similar to a finger snap. Kinematic analysis of high-speed video revealed that snap-jaw ant mandibles complete their strike in as little as 23 µsec and reach peak velocities of 90 m s^-1, making them the fastest known animal appendage. Finite-element analysis demonstrated that snap-jaw mandibles were less stiff than biting non-power-amplified mandibles, consistent with their use as a flexible spring. These results extend our understanding of animal speed and demonstrate how small changes in morphology can result in dramatic differences in performance.

Keywords: ants; finite-element analysis; functional morphology; microCT; power amplification.

Figure 1.

Morphology of the snap-jaw Dracula ant, Mystrium camillae. (a) Still image of a major worker with mandible tips touching in preparation for a strike. (b) Three-dimensional surface rendering of the head (grey), mandible (brown), adductor muscle (yellow), and abductor muscle (blue) involved in mandible movement. (c) Surface model of the mandible displaying some measurements for kinematic analysis and parameters for finite-element analysis. Blue dots represent points of finite-element model constraint (ventral condyle not visible). d, in-lever length between mandible centre of rotation and point of muscle attachment; F_add, force applied to mandible by mandible adductor muscle; r, mandible length.

Figure 2.

Ant mandibles compared with finite-element analysis. (a) Simplified surface models, and (b) cross-sections of three ant mandible specimens: the snap-jaw ant Mystrium camillae major worker, M. camillae minor worker, and the biting jaw ant, Stigmatomma pallipes. (c) Surface renderings of the head (transparent grey), mandible (brown), mandible adductor muscle (yellow), and mandible abductor (blue) of each specimen. Cross-sections are taken from the mandible bases. Scale bars: (a) and (b) = 0.1 mm, (c) = 1.0 mm.

Figure 3.

Loading phase and displacement of Mystrium mandibles prior to a strike. (a) Still images from high-speed video of the loading phase of a strike displaying the mandible in an unloaded (top) and loaded (bottom) state. Dots indicate the fixed landmarks (yellow) and semi-landmarks (white) used in two-dimensional geometric morphometric analysis. (b) Loaded finite-element model of striking mandible. Colours correspond to the amount of displacement of each brick element. Scale bar = 0.5 mm.

Figure 4.

Snap jaw kinematics. Left—Still images from a high-speed video of a representative M. camillae major worker mandible snap. The time elapsed since the beginning of mandible movement is given. Right—Kinematic profiles of the left (solid line) and right (dashed line) mandible derived from a high-speed video of a single mandible snap. Displacement (top panel) of the mandible tips (filled and open circles) was calculated from their x-y coordinates and smoothed with an interpolated spline. Angular velocity (middle panel) and angular acceleration (bottom panel) were calculated as the first and second derivative, respectively, of the smoothed displacement data. See main text for description of major events during strike and table 1 for means and variance across samples.

Figure 5.

Principle component analysis of mandible shape during loading. Procrustes-aligned two-dimensional landmarks clustered in two different groups in morphospace: unloaded mandibles at the beginning of a strike that had not yet deformed (blue), and loaded mandibles immediately prior to the strike (red). The shapes of unloaded and loaded mandibles from the finite-element models are displayed in yellow. Thin plate splines (below) display the minimum and maximum shapes of the first principle component which accounted for 65.7% of the total shape variance.

Figure 6.

Comparison of snap-jaw and biting mandible morphology. Finite-element models for (a) M. camillae major worker, (b) M. camillae minor worker, and (c) S. pallipes worker. All models were scaled to the same surface area to compare stress. Dorsal (left) and medial (right) views of each mandible displays the distribution of von Mises stresses. Peak von Mises stress and total strain energy are listed below. Contour plots are scaled to von Mises stress between 0 and 250 MPa.