Hippocampal Neurogenesis Reduces the Dimensionality of Sparsely Coded Representations to Enhance Memory Encoding

Abstract

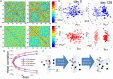
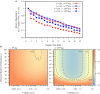
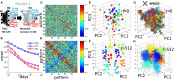
Adult neurogenesis in the hippocampal dentate gyrus (DG) of mammals is known to contribute to memory encoding in many tasks. The DG also exhibits exceptionally sparse activity compared to other systems, however, whether sparseness and neurogenesis interact during memory encoding remains elusive. We implement a novel learning rule consistent with experimental findings of competition among adult-born neurons in a supervised multilayer feedforward network trained to discriminate between contexts. From this rule, the DG population partitions into neuronal ensembles each of which is biased to represent one of the contexts. This corresponds to a low dimensional representation of the contexts, whereby the fastest dimensionality reduction is achieved in sparse models. We then modify the rule, showing that equivalent representations and performance are achieved when neurons compete for synaptic stability rather than neuronal survival. Our results suggest that competition for stability in sparse models is well-suited to developing ensembles of what may be called memory engram cells.

Keywords: dimensionality reduction; feed-forward neural network; hippocampus; neuromorphic computing; pattern separation; synaptic plasticity; synaptic pruning; synaptic turnover.

Figure 1

Neurogenesis enhances generalization performance. (A) In Model 1, after a weight vector is assigned by training, DG units with weak weights to CA3 are replaced with new randomly connected units. (B) At each day of training the network is tested with randomly generated patterns belonging to one of the two contexts. This generalization error decreases as a function of the number of iterations of neural turnover. Single simulation (gray) and mean of many simulations (black), before (red point) and after (orange point) neurogenesis. (C,D) CA3 Synaptic current distribution for all test patterns representing the two contexts before (C) and after (D) 128 iterations (days) of neural turnover. Results are from a network of 200 EC, 500 DG neurons and a single CA3 readout. Each context consists of 50 EC patterns with input noise, ν, fixed at 0.2, and theta is chosen to yield a coding level of f = 0.04, turnover rate is fixed at 0.30 (See Experimental Procedures). (E) Mean error is shown decreasing as a function of the number of iterations of neural turnover for three different coding levels. (F) Error is shown as a function of coding level before and after 128 iterations of neural turnover. After neurogenesis the performance is improved at all levels of sparseness (all coding levels, f). (G) The coding level at which minimum error occurs (optimal f) is plotted vs. the number of iterations of neural turnover. Neural turnover favor a sparser (reduced) coding level. Mean error is calculated as the mean of 20 simulations.

Figure 2

Neurogenesis exploits the low noise of the sparse code to outperform dense DG coding. (A) Distribution of CA3 current at t = 0 (before) vs. t = 128 (after) for the dense activity case of f = 0.5 for a group of test patterns generated from a single prototype pattern belonging to the (+) context. Vertical dashed line at 0 represents the activity threshold of the CA3 neuron (B) Same as in (A), but for the sparse case of f = 0.04. (C,D) Normalized CA3 readout weight distribution in dense (C) and sparse (D) cases. (E) Signal at CA3 vs. time for f = 0.5 (blue) and f = 0.04 (red). (F) Readout noise at CA3 vs. time for f = 0.5 (blue) and f = 0.04 (red). (G) Signal to noise ratio (SNR), calculated as data in (E) over data in (F). Demonstrates the advantage given by slower scaling of variance in the sparse case of f = 0.04. The results are plotted as the mean of 20 simulations.

Figure 3

Neurogenesis clusters context representations in DG activity space. (A) Matrix of pairwise correlations between training patterns represented in the DG, ordered by context so that patterns 1–50 correspond to the (+) context and patterns 51–100 correspond to (-) context. For a single simulation the correlation matrix of patterns for f = 0.50 before (left) and after (right) 128 iterations of neural turnover. (B) Same as in (A) but for f = 0.04. (C) Training patterns from the two contexts are projected onto the principal components. For visual clarity only the means of all training patterns for each of the 100 prototypes are projected. Closed and open circles correspond to the (+) and (-) contexts, respectively. Dense coding, f = 0.50, before (left) and after (right) 128 iterations of neural turnover. (D) as in (C) but for sparse coding of f = 0.04. (E) Mean correlation between patterns of opposite contexts (between) and patterns of the same context (within), calculated as mean of 20 simulations. (F) Schematic illustration of context discrimination by neurogenesis. Closed and open circles represent the patterns of the two respective contexts. Intuitively, as neuronal turnover and retraining proceeds the patterns in DG space are shifted in dimensions that are mostly parallel to the weight vector, over time leading to greater separation. All above results are from a single simulation.

Figure 4

Dimensionality reduction due to neurogenesis. (A) Relative magnitudes of ranked singular values, λ(i)/λ(1). The singular values are calculated for the centered DG activity matrix for a single simulation. In both cases the relative magnitudes of singular values drop after turnover of DG neurons. The sparse case (f = 0.04) shows larger drops than the dense case (f = 0.50). (B) Color-maps of classification error comparing predefined coding level, f, and restricted dimension d at different times, t = 0th day and t = 128th day. The number of dimensions used to calculate W is restricted to d, according to Equation (28). The error is the average error measured from 20 simulations. Before neuronal turnover, the map is relatively flat. After neuronal turnover there is a large region of low dimensionality over which the classification performance of the network maintains low error. Dashed line: contour for err = 0.15. Dot-Dashed Curve: contour for err = 0.20. Dotted line: contour for err = 0.25.

Figure 5

Selection of context-biased DG units takes advantage of the singular value distribution of the sparse code. (A,B) DG-CA3 weight vs. context-bias of individual DG neurons before and after neurogenesis for f = 0.50 (A) and f = 0.04 (B). Marginal histograms show the projected distributions. In both cases the DG-CA3 weights and the context-bias of DG neuron evolve to a bimodal distribution in which they are correlated. (C) Inverse square singular values, ${\sigma }_i^{-2}$, sorted by index, i. (D) The influence of the context-bias vector on the weight vector is determined by the relationship between $2P{\sigma }_i^{-2}\Vert {\widehat{\text{Ψ}}}_i\Vert$ and $\Vert {\widehat{\text{Ψ}}}_i\Vert$ over time. Plot shows the dense case (f = 0.50) and sparse case (f = 0.10) before and after neuronal turnover (128 iterations). (E) ‖W‖ grows more rapidly as a function of ‖Ψ‖ in the sparse case. Arrows label the direction of evolution. (F) W^TΨ grows more rapidly in the sparse case than in the dense case as a function of the product ‖W‖‖Ψ‖. Arrow labels the direction of evolution. (G) W^TΨ grows more rapidly in time in the sparse case, and determines the scale up of the SNR. All results are calculated from a single simulation. (H) Dense coding (blue, top) results in a reduced contribution of separating components, ${\sigma }_i^{-2}$ while sparse coding (red, bottom) results in less reduction in the contribution of these components, promoting greater separation of contexts in DG activity space.

Figure 6

Neuronal turnover rule can be generalized to encode multiple contexts. (A) In Model 2, multiple context discrimination is performed by using multiple readout units each with trained weights. The turnover rule sums the absolute readout weights of all units and eliminates the units ranking in the bottom 30%. (B) Generalization error decreases with neurogenesis, and the sparse code is optimal for the multicontext case, shown as the mean of 20 simulations (input noise, ν = 0.05, 12 prototypes per context). (C) For a single simulation, pairwise correlation matrix of patterns in DG space before neurogenesis. (D) Same as in (C) after 512 days of neurogenesis. Patterns evolve into correlated groups in DG space. (E) Projection of patterns in DG space onto PCs, before neurogenesis. (F) Same as in (E) after 512 iterations of neurogenesis. Clusters emerge from a random arrangement, and move apart from each other. (G) As in (E) but projection of test patterns onto PCs, day 0 before neurogenesis. (H) as in (G) but after day 512 of neurogenesis. Patterns representing distinct contexts cluster together, and become separated from each other.

Figure 7

A synaptic turnover rule generalizes neuronal turnover to allow prediction of biological rates. (A) In Model 3, the strength of a DG neurons weight to CA3 is used to determine the probability of turnover of EC-DG synapses onto that neuron. (B) Error vs. time for synaptic turnover model with slope set to 2.5, is similar to Model 1 in which a fixed fraction of 0.30 DG units are turned over. (C) the optimal coding level is between 4 and 5% as in the prior model. (D) Fraction of synapses turned over as a function of time for different coding levels, f. The sparsely coded DG requires greater synaptic turnover. Yet Model 3, for all f, requires less turnover than Model 1 (dotted black line) for a similar level of performance. (E) Fraction of neurons turned over vs. time. The sparse case requires more DG units to be turned over. (F) For each time point, the coding level at which optimal performance is achieved is evaluated, and plotted as optimal coding level. The optimal coding level becomes more sparse in time as in Model 1 and 2. (G) The tradeoff between cumulative synaptic turnover vs. cumulative reduction in error is best resolved by the sparse DG. (H) same as in G but for neural turnover. (I) Cumulative neuronal replacement of DG vs. time, corresponding well with experimental data suggesting around 10% of the mature DG is replaced by adult-born cells (Imayoshi et al., 2008). All results are calculated as the mean of 100 simulations, with slope = 2.5 for the linear transfer function (See Experimental Procedures). See also Figure S1.