Colloidal Model for the Prediction of the Extraction of Rare Earths Assisted by the Acidic Extractant

Abstract

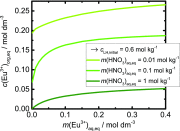
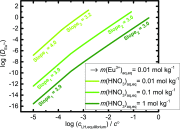
We propose the statistical thermodynamic model for the prediction of the liquid-liquid extraction efficiency in the case of rare-earth metal cations using the common bis(2-ethyl-hexyl)phosphoric acid (HDEHP) extractant. In this soft matter-based approach, the solutes are modeled as colloids. The leading terms in free-energy representation account for: the complexation, the formation of a highly curved extractant film, lateral interactions between the different extractant head groups in the film, configurational entropy of ions and water molecules, the dimerization, and the acidity of the HDEHP extractant. We provided a full framework for the multicomponent study of extraction systems. By taking into account these different contributions, we are able to establish the relation between the extraction and general complexation at any pH in the system. This further allowed us to rationalize the well-defined optimum in the extraction engineering design. Calculations show that there are multiple extraction regimes even in the case of lanthanide/acid system only. Each of these regimes is controlled by the formation of different species in the solvent phase, ranging from multiple metal cation-filled aggregates (at the low acid concentrations in the aqueous phase), to the pure acid-filled aggregates (at the high acid concentrations in the aqueous phase). These results are contrary to a long-standing opinion that liquid-liquid extraction can be modeled with only a few species. Therefore, a traditional multiple equilibria approach is abandoned in favor of polydisperse spherical aggregate formations, which are in dynamic equilibrium.

Figure 1

Schematic representation of the extraction process. Various types of aggregates are present in the solvent, and their probability at equilibrium is determined by the composition of their cores. Considering the surfactant nature of the extractant, the interface is at least partially covered by the extractant molecules (not shown here). The zoomed region shows the core of the aggregate with the europium cation, the nitrate anion, and the extractant head groups, i.e., phosphate groups.

Figure 2

Concentrations of solutes in an organic solvent as a function of the initial extractant concentration, c_LH,initial. The solvent phase in contact with (a) pure water, (b) HNO₃ aqueous solution, m(HNO₃)_aq,eq = 1 mol kg^–1, (c) Eu(NO₃)₃, HNO₃ aqueous solution, m(HNO₃)_aq,eq = 1 mol kg^–1 and m(Eu³⁺)_aq,eq = 0.032 mol kg^–1.

Figure 3

Negative value of the natural logarithm of the Eu³⁺ distribution coefficient, −ln D_Eu³⁺, as a function of the Eu³⁺ complexation energy parameter per bond, E_0,Eu³⁺, and the exchange parameter, χ_LH,L^–, used in the calculations. The white region depicts the experimental data.

Figure 4

Speciation of the extractant in the solvent as a function of the initial extractant concentration, c_LH,initial. The solvent phase is in contact with m(HNO₃)_aq,eq = 1 mol kg^–1 and m(Eu³⁺)_aq,eq = 0.032 mol kg^–1. Enlarged region at low c_LH,initial is presented in the inset.

Figure 5

Speciation of the extractant in the solvent as a function of HNO₃ concentration m(HNO₃)_aq,eq in the aqueous phase and the initial extractant concentration c_LH,monomer in the solvent: (a) aggregated extractant, (b) dimerized, (c) monomeric, (d) equivalent to (c), but the scale is adjusted so that differences in c_LH,monomer can be clearly seen. The europium concentration used for the calculation is m(Eu³⁺)_eq,aq = 0.032 mol kg^–1, and c_LH,initial = 0.6 mol dm^–3.

Figure 6

Eu³⁺ distribution coefficient, D_Eu³⁺, as a function of HNO₃ concentration in the aqueous phase. Results for the various initial extractant concentrations, c_LH,initial, are presented. The solvent phase is in contact with m(Eu³⁺)_aq,eq = 0.05 mol kg^–1.

Figure 7

Eu³⁺ concentration in the solvent as a function of europium concentration in the aqueous phase, m(Eu³⁺)_aq,eq. Results for various m(HNO₃)_aq,eq and c_LH,initial = 0.6 mol dm^–3 are presented.

Figure 8

Decimal logarithm of Eu³⁺ distribution coefficient as a function of the sum of the amount of monomeric and dimerized extractants at equilibrium, log(c_{LH,equilibrium}/c°); c_{LH,equilibrium} = c_LH,monomer + 2c_LH,dimerized. The results for various m(HNO₃)_aq,eq and m(Eu³⁺)_aq,eq = 0.01 mol kg^–1 are presented.

Figure 9

Concentrations of the extracted solutes (a–c) and CAC (d) in the solvent phase as a function m(Eu³⁺)_aq,eq and m(HNO₃)_aq,eq. Results are presented for the case of c_LH,initial = 0.6 mol dm^–3. The inset in (a) shows an enlarged region of the pronounced Eu³⁺ extraction.

Figure 10

Apparent energy of Eu³⁺ transfer as a function of the negative value of the complexation energy parameter per bond, −E_0,Eu³⁺. The negative values of E_0,Eu³⁺ are taken for the purpose of visually easier reading of the saturation limit. Results for various m(HNO₃)_aq,eq are presented at m(Eu³⁺)_aq,eq = 0.05 mol kg^–1 and c_LH,initial = 0.6 mol dm^–3. The dashed orange line represents the assumption that the apparent energy of transfer is equal to the total complexation energy in the aggregate.

Figure 11

Negative value of the natural logarithm of the Eu³⁺ distribution coefficient, −ln D_Eu³⁺, as a function of −E_0,Eu³⁺ and m(Eu³⁺)_aq,eq. The results are presented for various m(HNO₃)_aq,eq for c_LH,initial = 0.6 mol dm^–3. The white region depicts the experimental data. The dotted rectangle enclosing the white region is given as a guideline to depict its broadness.