Microscale to mesoscale analysis of parenchymal tethering: the effect of heterogeneous alveolar pressures on the pulmonary mechanics of compliant airways

Abstract

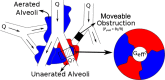
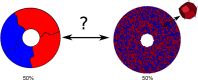
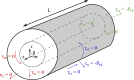
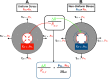
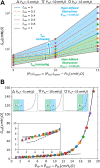
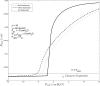
In the healthy lung, bronchi are tethered open by the surrounding parenchyma; for a uniform distribution of these peribronchial structures, the solution is well known. An open question remains regarding the effect of a distributed set of collapsed alveoli, as can occur in disease. Here, we address this question by developing and analyzing microscale finite-element models of systems of heterogeneously inflated alveoli to determine the range and extent of parenchymal tethering effects on a neighboring collapsible airway. This analysis demonstrates that micromechanical stresses extend over a range of ∼5 airway radii, and this behavior is dictated primarily by the fraction, not distribution, of collapsed alveoli in that region. A mesoscale analysis of the microscale data identifies an effective shear modulus, G_eff, that accurately characterizes the parenchymal support as a function of the average transpulmonary pressure of the surrounding alveoli. We demonstrate the use of this formulation by analyzing a simple model of a single collapsible airway surrounded by heterogeneously inflated alveoli (a "pig-in-a-blanket" model), which quantitatively demonstrates the increased parenchymal compliance and reduction in airway caliber that occurs with decreased parenchymal support from hypoinflated obstructed alveoli. This study provides a building block from which models of an entire lung can be developed in a computationally tenable manner that would simulate heterogeneous pulmonary mechanical interdependence. Such multiscale models could provide fundamental insight toward the development of protective ventilation strategies to reduce the incidence or severity of ventilator-induced lung injury. NEW & NOTEWORTHY A destabilized lung leads to airway and alveolar collapse that can result in catastrophic pulmonary failure. This study elucidates the micromechanical effects of alveolar collapse and determines its range of influence on neighboring collapsible airways. A mesoscale analysis reveals a master relationship that can that can be used in a computationally efficient manner to quantitatively model alveolar mechanical heterogeneity that exists in acute respiratory distress syndrome (ARDS), which predisposes the lung to volutrauma and/or atelectrauma. This analysis may lead to computationally tenable simulations of heterogeneous organ-level mechanical interactions that can illuminate novel protective ventilation strategies to reduce ventilator-induced lung injury.

Keywords: acute respiratory distress syndrome; mechanical ventilation; parenchymal tethering; reduced-dimension model; shear modulus.

Fig. 1.

Representative illustration of airway obstruction resulting in the presence of aerated (blue) and obstructed (red) alveoli surrounding separate conducting airways. G_eff, effective shear modulus; P_yield, critical pressure drop.

Fig. 2.

Approximation of heterogeneous tethering using a uniformly random distribution of obstructed alveoli (“sprinkled donut”).

Fig. 3.

Boundary conditions of finite-element model (FEM) on the fixed face (red), cylindrical face (blue), and free-moving face (green). The interior hole is assumed to be at a constant pressure (P_PA), as shown in Fig. 4.

Fig. 4.

A: parenchyma in equilibrium uniform stressed state. B: change in hole lumen with change in peri-airway pressure (P_PA) from the uniform stress condition pleural pressure (P_PL).

Fig. 5.

Calculation of the effective shear modulus (G_eff) as a function of the region of influence (ROI) scaled by the “hole” radius (R_H).

Fig. 6.

Comparison of localization of obstructed alveoli and heterogeneous distribution. Error bars represent the standard deviation. G_eff, shear modulus.

Fig. 7.

A: shear modulus (G_eff) as a function of transpulmonary pressure (P_TP) with aerated alveoli (P_ALV)_open = 0 and hyperinflated obstructed alveoli (P_OBS) = +4 cmH₂O (shaded blue) or hypoinflated obstructed alveoli P_OBS = −4 cmH₂O (shaded green) for pleural pressure (P_PL)  = −5 cmH₂O (△), P_PL = −10 cmH₂O (▽), and P_PL = −15 cmH₂O (○). Fraction of obstructed alveoli varies over 0 ≤ f_OBS ≤ 1. B: shear modulus (G_eff) as a function of the weighted average transpulmonary pressure.

Fig. 8.

Simple airway model of conducting airway surrounded by parenchyma with heterogeneously distributed obstructed alveoli. P_AW, airway pressure; R_AW, airway radius;

Fig. 9.

Tube law at the trachea (z = o) and an airway at the 16th generation (z = 16).

Fig. 10.

Simulation of a collapsible 16th generation airway without parenchymal support (solid line), with parenchymal support (dashed line), and with parenchymal support from hypoinflated obstructed alveoli (P_OBS = −2.5 cmH₂O, f_OBS = 1, dotted line). P_PL = −5 cmH₂O, γ = 50 mN/m.