Scale-Change Symmetry in the Rules Governing Neural Systems
- PMID: 30682624
- PMCID: PMC6352707
- DOI: 10.1016/j.isci.2019.01.009
Scale-Change Symmetry in the Rules Governing Neural Systems
Abstract
Similar universal phenomena can emerge in different complex systems when those systems share a common symmetry in their governing laws. In physical systems operating near a critical phase transition, the governing physical laws obey a fractal symmetry; they are the same whether considered at fine or coarse scales. This scale-change symmetry is responsible for universal critical phenomena found across diverse systems. Experiments suggest that the cerebral cortex can also operate near a critical phase transition. Thus we hypothesize that the laws governing cortical dynamics may obey scale-change symmetry. Here we develop a practical approach to test this hypothesis. We confirm, using two different computational models, that neural dynamical laws exhibit scale-change symmetry near a dynamical phase transition. Moreover, we show that as a mouse awakens from anesthesia, scale-change symmetry emerges. Scale-change symmetry of the rules governing cortical dynamics may explain observations of similar critical phenomena across diverse neural systems.
Keywords: Mathematical Biosciences; Statistical Mechanics; Systems Neuroscience.
Copyright © 2019 The Author(s). Published by Elsevier Inc. All rights reserved.
Figures

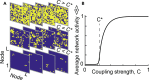

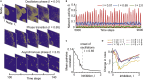

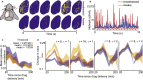

References
-
- Arieli A., Sterkin A., Grinvald A., Aertsen A. Dynamics of ongoing activity: explanation of the large variability in evoked cortical responses. Science. 1996;273:1868–1871. - PubMed
-
- Brunel N. Dynamics of networks of randomly connected excitatory and inhibitory spiking neurons. J. Physiol. 2000;94:445–463. - PubMed

