Conflict and accord of optimal treatment strategies for HIV infection within and between hosts

Abstract

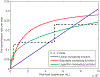
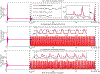
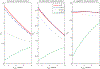
Most of previous studies investigated the optimal control of HIV infection at either within-host or between-host level. However, the optimal treatment strategy for the individual may not be optimal for the population and vice versa. To determine when the two-level optimal controls are in accord or conflict, we develop a multi-scale model using various functions that link the viral load within host and the transmission rate between hosts, calibrated by cohort data. We obtain the within-host optimal treatment scheme that minimizes the viral load and maximizes the count of healthy cells at the individual level, and the coupled optimal scheme that minimizes the basic reproduction number at the population level. Mathematical analysis shows that whether the two-level optimal controls coincide depends on the sign of the product of their switching functions. Numerical results suggest that they are in accord for a high maximal drug efficacy but may conflict for a low drug efficacy. Using the multi-scale model, we also identify a threshold of the treatment effectiveness that determines how early treatment initiation can affect the disease dynamics among population. These results may help develop a synergistic treatment protocol beneficial to both HIV-infected individuals and the whole population.

Keywords: HIV Infection; Multi-scale model; Optimal treatment strategy; Treatment accord; Treatment conflict.

Fig. 1.

The dependence of the annual transmission rate per partnership on viral load. Three increasing functions are used to describe this relationship: case (i) linear function (blue line), case (ii) saturated function (red line), and case (iii) logarithm function (green line). The linear and logarithm functions are fitted to the data (black dashed line) from [11,39,57], and the saturated case, which has been estimated in [11], is shown for comparison.

Fig. 2.

The optimal treatment schedule at the within-host $({\eta }_0^{\ast }(a))$ and coupled (η*(a)) level. If the maximal drug efficacy η_max is 0.9, the optimal controls at the two levels are in accord $({\eta }^{\ast }(a)={\eta }_0^{\ast }(a)={\eta }_{\max }=0.9)$ for all three cases (see Table 2 for optimal objective values) and shown in the same color (green lines). If the maximal drug efficacy η_max is 0.5, the within-host optimal control ${\eta }_0^{\ast }(a)$ (blue dashed lines, which can be regarded as always keeping maximal drug efficacy, i.e., ${\eta }_0^{\ast }(a)={\eta }_{\max }=0.5$, because their objective values J₀ are very close as shown in Table 3) is in accord with the coupled optimal control in the linear case (red solid line in subfigure (a), which can also be treated as η*(a) = η_max = 0.5 because of almost same objective values J in Table 3), but in conflict with two other coupled optimal control (red solid lines in subfigure (b) for the saturated case and in subfigure (c) for the logarithm case). The insets show zoomed optimal control for a slice of the time-series. ART initiation timing is fixed as a_ART = 5 years. The time A (corresponding to black dashed lines) denotes when the AIDS stage begins, i.e., the time when infectious period ends, based on the assumption that AIDS patients do not contribute to the transmission of HIV [17].

Fig. 3.

The survival probability σ(a) (see Appendix B) corresponding to the optimal treatment schedule at the within-host level ${\eta }_0^{\ast }(a)$ and coupled level η*(a) in Fig. 2 for three cases (i)–(iii) in Fig. 1. The survival probability corresponding to the within-host optimal control (blue dashed lines) is equal to (a) or higher (b and c) than that for the coupled optimal control (red solid lines) when the maximal drug efficacy is η_max = 0.5. The insets show zoomed survival probability for a slice of the time-series. The time a_ART and A are the same as in Fig. 2.

Fig. 4.

Viral load corresponding to the optimal treatment schedule at the within-host level ${\eta }_0^{\ast }(a)$ and coupled level η*(a) in Fig. 2 for three cases (i)–(iii) in Fig. 1. The insets show zoomed viral load for a slice of the time-series. The time a_ART and A are the same as in Fig. 2.

Fig. 5.

The annual transmission rate per partnership corresponding to the optimal treatment schedule at the within-host level ${\eta }_0^{\ast }(a)$ and coupled level η*(a) in Fig. 2 for three cases (i)–(iii) in Fig. 1. The insets show zoomed transmission rate for a slice of the time-series. The time a_ART and A are the same as in Fig. 2.

Fig. 6.

Plots of the basic reproduction number R₀, consisting of the contribution of individuals before treatment R₀₁ and under treatment R₀₂, versus the drug efficacy η (assumed to be a constant) for the linear case (a–c), saturated case (d–f), and logarithm case (g–i), respectively. The ART initiating timing a_ART is chosen as 1 year (red solid lines), 5 years (green dashed lines), and 8 years (blue dash-dot lines). All the other parameters are listed in Table 1.

Fig. 7.

The effect of ART initiation timing a_ART on the basic reproduction number R₀ when the constant drug efficacy η is chosen as 0 (red solid lines), 0.4 (blue dashed lines), 0.8 (black dotted lines), and 0.9 (green dash-dot lines). All the other parameters are listed in Table 1.