Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2019 Apr 1;188(4):632-636.
doi: 10.1093/aje/kwz013.

Nonparametric Bounds for the Risk Function

Stephen R Cole  1 , Michael G Hudgens  2 , Jessie K Edwards  1 , M Alan Brookhart  1   3 , David B Richardson  1 , Daniel Westreich  1 , Adaora A Adimora  1   4
Affiliations

Nonparametric Bounds for the Risk Function

Stephen R Cole et al. Am J Epidemiol. .

Abstract

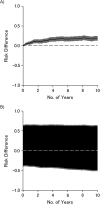
Nonparametric bounds for the risk difference are straightforward to calculate and make no untestable assumptions about unmeasured confounding or selection bias due to missing data (e.g., dropout). These bounds are often wide and communicate uncertainty due to possible systemic errors. An illustrative example is provided.

Keywords: bias; bounds; inference; missing data.

PubMed Disclaimer

Figures

Figure 1.
Figure 1.
Difference in risk of acquired immune deficiency syndrome diagnosis or death from any cause by injection drug use, as a function of time on study, Women’s Interagency HIV Study, United States, 1995–2006. Crude results (A); bounds for confounding and selection bias (B). Black line or area is the point or set estimate, and gray area is the 95% confidence interval. HIV, human immunodeficiency virus.
See this image and copyright information in PMC

References

    1. Robins JM. The analysis of randomized and nonrandomized AIDS treatment trials using a new approach to causal inference in longitudinal studies In: Sechrest L, Freeman H, Mulley A, eds. Health Service Research Methodology: A Focus on AIDS. Washington, DC: US Public Health Service; 1989:113–15959.
    1. Manski CF. Nonparametric bounds on treatment effects. Am Econ Rev. 1990;80(2):319–323.
    1. Balke A, Pearl J. Bounds on treatment effects from studies with imperfect compliance. J Am Stat Assoc. 1997;92(439):1171–1176.
    1. Robins JM. Confidence intervals for causal parameters. Stat Med. 1988;7(7):773–785. - PubMed
    1. Cole SR, Frangakis CE. The consistency statement in causal inference: a definition or an assumption? Epidemiology. 2009;20(1):3–5. - PubMed

Publication types