Molecular Complexity Calculated by Fractal Dimension

Abstract

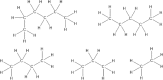
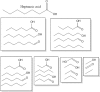
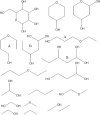
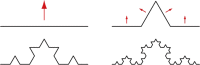
Molecular complexity is an important characteristic of organic molecules for drug discovery. How to calculate molecular complexity has been discussed in the scientific literature for decades. It was known from early on that the numbers of substructures that can be cut out of a molecular graph are of importance for this task. However, it was never realized that the cut-out substructures show self-similarity to the parent structures. A successive removal of one bond and one atom returns a series of fragments with decreasing size. Such a series shows self-similarity similar to fractal objects. Here we used the number of distinct fragments to calculate the fractal dimension of the molecule. The fractal dimension of a molecule is a new matter constant that incorporates all features that are currently known to be important for describing molecular complexity. Furthermore, this is the first work that reveals the fractal nature of organic molecules.

Figure 1

n-Hexane and four distinct alkanes obtained by successively removing one bond and one atom, followed by saturation with hydrogen.

Figure 2

Heptanoic acid and its distinct substructures. Grouped by bond counts.

Figure 3

Glucose and some of its distinct subgraphs. Subgraphs A and B are shown twice in both bent and elongated forms.

Figure 4

Koch curve.

Figure 5

n-Hexane in line notation, covered by boxes for the box counting algorithm.

Figure 6

The number of distinct subgraphs (N) for five example organic molecules versus the bond count of the subgraphs (γ). The numbers of distinct subgraphs on the y-axis are given in logarithmic scale.