Near-equilibrium isotope fractionation during planetesimal evaporation
- PMID: 30739951
- PMCID: PMC6364317
- DOI: 10.1016/j.icarus.2019.01.012
Near-equilibrium isotope fractionation during planetesimal evaporation
Abstract
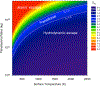
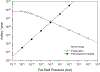
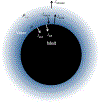
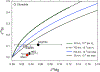
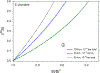
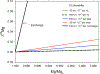
Silicon and Mg in differentiated rocky bodies exhibit heavy isotope enrichments that have been attributed to evaporation of partially or entirely molten planetesimals. We evaluate the mechanisms of planetesimal evaporation in the early solar system and the conditions that controled attendant isotope fractionations. Energy balance at the surface of a body accreted within ~1 Myr of CAI formation and heated from within by 26Al decay results in internal temperatures exceeding the silicate solidus, producing a transient magma ocean with a thin surface boundary layer of order < 1 meter that would be subject to foundering. Bodies that are massive enough to form magma oceans by radioisotope decay (≥ 0.1% M ⊕) can retain hot rock vapor even in the absence of ambient nebular gas. We find that a steady-state rock vapor forms within minutes to hours and results from a balance between rates of magma evaporation and atmospheric escape. Vapor pressure buildup adjacent to the surfaces of the evaporating magmas would have inevitably led to an approach to equilibrium isotope partitioning between the vapor phase and the silicate melt. Numerical simulations of this near-equilibrium evaporation process for a body with a radius of ~ 700 km yield a steady-state far-field vapor pressure of 10-8 bar and a vapor pressure at the surface of 10-4 bar, corresponding to 95% saturation. Approaches to equilibrium isotope fractionation between vapor and melt should have been the norm during planet formation due to the formation of steady-state rock vapor atmospheres and/or the presence of protostellar gas. We model the Si and Mg isotopic composition of bulk Earth as a consequence of accretion of planetesimals that evaporated subject to the conditions described above. The results show that the best fit to bulk Earth is for a carbonaceous chondrite-like source material with about 12% loss of Mg and 15% loss of Si resulting from near-equilibrium evaporation into the solar protostellar disk of H2 on timescales of 104 to 105 years.
Keywords: Asteroids; Cosmochemistry; Planetesimals; composition.
Conflict of interest statement
Declarions of interest: none
Figures
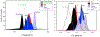
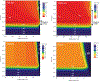

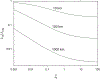

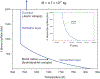

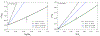


References
-
- Alexander CMOD (2001) Exploration of quantitative kinetic models for the evaporation of silicate melts in vacuum and in hydrogen. Meteoritical & Planetary Science 36: 255–283
-
- Carslaw HS and Jaeger JC (1959). Conduction of Heat in Solids Oxford, Clarendon Press.
-
- Carter PJ, Leinhardt Z, Elliott T, Walter MJ and Stewart ST (2015) Compositional evolution during rocky protoplanet accretion. The Astrophysical Journal 813: doi:10.1088/0004-1637x/1813/1081/1072 - DOI
-
- Courtial P and Dingwell DB (1999) Densities of melts in the CaO-MgO-Al2O3-SiO2 system. American Mineralogist 84: 465–476
