Cerebrovascular Smooth Muscle Cells as the Drivers of Intramural Periarterial Drainage of the Brain
- PMID: 30740048
- PMCID: PMC6357927
- DOI: 10.3389/fnagi.2019.00001
Cerebrovascular Smooth Muscle Cells as the Drivers of Intramural Periarterial Drainage of the Brain
Abstract
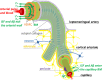
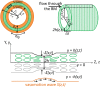
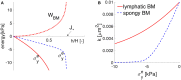
The human brain is the organ with the highest metabolic activity but it lacks a traditional lymphatic system responsible for clearing waste products. We have demonstrated that the basement membranes of cerebral capillaries and arteries represent the lymphatic pathways of the brain along which intramural periarterial drainage (IPAD) of soluble metabolites occurs. Failure of IPAD could explain the vascular deposition of the amyloid-beta protein as cerebral amyloid angiopathy (CAA), which is a key pathological feature of Alzheimer's disease. The underlying mechanisms of IPAD, including its motive force, have not been clarified, delaying successful therapies for CAA. Although arterial pulsations from the heart were initially considered to be the motive force for IPAD, they are not strong enough for efficient IPAD. This study aims to unravel the driving force for IPAD, by shifting the perspective of a heart-driven clearance of soluble metabolites from the brain to an intrinsic mechanism of cerebral arteries (e.g., vasomotion-driven IPAD). We test the hypothesis that the cerebrovascular smooth muscle cells, whose cycles of contraction and relaxation generate vasomotion, are the drivers of IPAD. A novel multiscale model of arteries, in which we treat the basement membrane as a fluid-filled poroelastic medium deformed by the contractile cerebrovascular smooth muscle cells, is used to test the hypothesis. The vasomotion-induced intramural flow rates suggest that vasomotion-driven IPAD is the only mechanism postulated to date capable of explaining the available experimental observations. The cerebrovascular smooth muscle cells could represent valuable drug targets for prevention and early interventions in CAA.
Keywords: Alzheimer's disease; brain; cerebral amyloid angiopathy; lymphatic; multi-scale model; perivascular drainage; poroelastic; vasomotion.
Figures
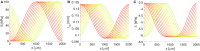
References
-
- Albargothy N. J., Johnston D. A., MacGregor-Sharp M., Weller R. O., Verma A., Hawkes C. A., et al. . (2018). Convective influx/glymphatic system: tracers injected into the csf enter and leave the brain along separate periarterial basement membrane pathways. Acta Neuropathol. 136, 139–152. 10.1007/s00401-018-1862-7 - DOI - PMC - PubMed
LinkOut - more resources
Full Text Sources

