Efficient neural decoding of self-location with a deep recurrent network

Abstract

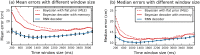
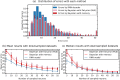
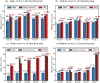
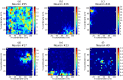
Place cells in the mammalian hippocampus signal self-location with sparse spatially stable firing fields. Based on observation of place cell activity it is possible to accurately decode an animal's location. The precision of this decoding sets a lower bound for the amount of information that the hippocampal population conveys about the location of the animal. In this work we use a novel recurrent neural network (RNN) decoder to infer the location of freely moving rats from single unit hippocampal recordings. RNNs are biologically plausible models of neural circuits that learn to incorporate relevant temporal context without the need to make complicated assumptions about the use of prior information to predict the current state. When decoding animal position from spike counts in 1D and 2D-environments, we show that the RNN consistently outperforms a standard Bayesian approach with either flat priors or with memory. In addition, we also conducted a set of sensitivity analysis on the RNN decoder to determine which neurons and sections of firing fields were the most influential. We found that the application of RNNs to neural data allowed flexible integration of temporal context, yielding improved accuracy relative to the more commonly used Bayesian approaches and opens new avenues for exploration of the neural code.

Fig 1. Accurate decoding of position with a RNN.

Location decoding errors based on CA1 neural data recorded from 1m square open field environment as a function of time window size. (a) shows mean error and (b) median error. Blue lines represent errors from the RNN decoder and red lines from Bayesian approaches. Results for the RNN approach are averaged over different independent realizations of the training algorithm. Black dots depict the mean/median error of each individual model. Results shown are for animal R2192.

Fig 2. Comparison of RNN and Bayesian decoders.

(a) Histogram of error sizes, generated in each case with the best performing time window (1400 ms for RNN, 2800 ms for flat Bayesian and 2000ms for Bayesian with memory). Both types of Bayesian decoders make more very large errors (0.02% vs 2.7% of errors > 50 cm). Errors are grouped into 2 cm bins, the last bin shows all errors above 50 cm. (b-c) Downsampling analysis demonstrates the RNN decoder is more robust to small dataset sizes. Data from R2192 was downsampled and all three decoders were trained with a random subset of the available neurons. For each sample size, 10 random sets of neurons were selected and independent models trained as before using 10-fold cross validation. Dots represents (b) mean and (c) median error for each downsampled dataset. Lines indicate the (b) mean of means and (c) mean of medians over sets of the same size.

Fig 3. Spatial decoding across animals in 2D and 1D environments.

(a-b) Decoding results in a 1m square environment. The RNN consistently outperforms the two Bayesian approaches in all 5 data sets. Mean and median errors across cross validation folds, respectively. (c-d) Decoding errors from a 600 cm long Z-shaped track. RNN consistently yields lower decoding errors than the Bayesian approaches, the difference is more marked when mean (c) as oppose to median (d) errors are considered.

Fig 4. Analysis of the errors in function of location and neural activity for rat R2192.

(a) The trajectory of the rat during the entire trial. Not all parts of the arena are visited with equal frequently. (b) The average size of errors made in different regions of space. Color of each hexagon depicts the average euclidean error of data points falling into the hexagon. More frequently visited areas (as seen from (a)) tend to have lower mean error. (c) Sum neural activity in different regions of space. For each data point we sum the spike counts of all 63 neurons in a 1400 ms period centered around the moment the location was recorded. The color of the hexagon corresponds to the average over all data points falling into the hexagon. Areas where sum neural activity is high have lower prediction error. (d) Prediction error of a coordinate decreases if the animal is closer to the wall perpendicular to that coordinate.

Fig 5. Results of knockout analysis.

The firing rate maps of the most (a-e) and least (f) influential neurons according to the knockout analysis. Colour bar to the right of each plot indicates the firing rate in Hz. With the complete dataset the mean error was 12.50±0.28 cm. When knocking out neurons 55, 26, 41, 17, 23 (the five most influential) and 9 (the least influential), the mean error increased to 14.72 cm, 13.80 cm, 13.66 cm, 13.50 cm, 13.49 cm and 12.58 cm respectively.

Fig 6. Gradient analysis: Sensitivity decreases with activity.

(a) Place field of an example neuron. (b) Sensitivity field—absolute values of gradients in different locations for the same neuron. (c) Normalized sensitivity as a function of normalized activity across neurons.

Fig 7. Feature extraction from spiking data and neural network architecture.

(a) Extracting a sequence of spike count vectors from spiking data. Each subsequent input originates from an overlapping time period, shifted 200 ms forward in time. (b) The input data that the RNN decoder will use is a sequence of spike count vectors from these time windows. (c) The network used for decoding consists of an input layer (size equals number of recorded neurons), two hidden layers containing 512 long-short term memory (LSTM) units and an output layer of size 2 (x and y coordinates). The spike count vectors are inserted to the input layer one by one at each timestep. The network produces a prediction for x and y coordinates only at the end of the sequence, at t = 100.