Nash Equilibria in the Response Strategy of Correlated Games

Abstract

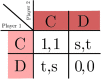
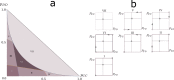
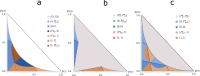
In nature and society, problems that arise when different interests are difficult to reconcile are modeled in game theory. While most applications assume that the players make decisions based only on the payoff matrix, a more detailed modeling is necessary if we also want to consider the influence of correlations on the decisions of the players. We therefore extend here the existing framework of correlated strategies by giving the players the freedom to respond to the instructions of the correlation device by probabilistically following or not following its suggestions. This creates a new type of games that we call "correlated games". The associated response strategies that can solve these games turn out to have a rich structure of Nash equilibria that goes beyond the correlated equilibrium and pure or mixed-strategy solutions and also gives better payoffs in certain cases. We here determine these Nash equilibria for all possible correlated Snowdrift games and we find these solutions to be describable by Ising models in thermal equilibrium. We believe that our approach paves the way to a study of correlations in games that uncovers the existence of interesting underlying interaction mechanisms, without compromising the independence of the players.

Figure 1

Normalized payoff table for two-by-two, symmetric games.

Figure 2

Symmetric correlations and associated equilibrium response strategies for the Snowdrift game with s = 0.5 and t = 1.2. (a) Illustration of all correlated Nash equilibria of the Snowdrift game in the P_CC − P_DD plane, for parameters representative of s > t − 1. (b) Schematic representation of the equilibrium value of the response probabilities in the P_FD − P_FC plane that can be found in each region enumerated in (a).

Figure 3

Equilibrium response strategies with highest payoff per region, for different parameters. (a) Equilibria corresponding to highest payoff by region, for s = 0.5 and t = 1.2 (s > t − 1), without the mixed-strategy solution. (b) Equilibria corresponding to highest payoff, for the same parameters as (a), including the mixed-strategy solution. (c) Equilibria corresponding to highest payoff by region, for s = 0.23 and t = 1.5 (s < t − 1), including the mixed-strategy solution. The existing equilibrium solutions are compared within a region, according to the description in Fig. 2. The darkening of the colors represents a higher absolute value of the payoff when compared to the best payoffs of the neighboring regions, but the actual value changes within the region, except for the mixed-strategy solution, of which the is constant. All the payoffs corresponding to the best solution are continuous to one another.