Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2019 Mar 15:256:91-104.
doi: 10.1016/j.dam.2018.03.071. Epub 2018 Apr 26.

Minimal NMR distance information for rigidity of protein graphs

Carlile Lavor  1 , Leo Liberti  2 , Bruce Donald  3 , Bradley Worley  4   5 , Benjamin Bardiaux  4   5 , Thérèse E Malliavin  4   5 , Michael Nilges  4   5
Affiliations

Minimal NMR distance information for rigidity of protein graphs

Carlile Lavor et al. Discrete Appl Math. .

Abstract

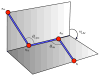
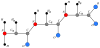
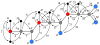
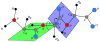
Nuclear Magnetic Resonance (NMR) experiments provide distances between nearby atoms of a protein molecule. The corresponding structure determination problem is to determine the 3D protein structure by exploiting such distances. We present a new order on the atoms of the protein, based on information from the chemistry of proteins and NMR experiments, which allows us to formulate the problem as a combinatorial search. Additionally, this order tells us what kind of NMR distance information is crucial to understand the cardinality of the solution set of the problem and its computational complexity.

Keywords: Distance geometry; Molecular structure; Nuclear magnetic resonance; Vertex orders.

PubMed Disclaimer

Figures

Fig. 1
Fig. 1
Cartesian and internal coordinates.
Fig. 2
Fig. 2
Protein backbone.
Fig. 3
Fig. 3
Geometric interpretation of branching in BP.
Fig. 4
Fig. 4
The hc order.
Fig. 5
Fig. 5
Peptide plane.
Fig. 6
Fig. 6
Chirality property.
See this image and copyright information in PMC

References

    1. Agra A, Figueiredo R, Lavor C, Maculan N, Pereira A, Requejo C. Feasibility check for the distance geometry problem: an application to molecular conformations. Int Trans Oper Res. 2017;24:1023–1040.
    1. Alves R, Lavor C. Geometric algebra to model uncertainties in the discretizable molecular distance geometry problem. Adv Appl Clifford Algebra. 2017;27:439–452.
    1. Alves R, Lavor C, Souza C, Souza M. Clifford algebra and discretizable distance geometry. Math Methods Appl Sci. 2018 doi: 10.1002/mma.4422. . in press. - DOI
    1. Anderson B, Belhumeur P, Eren T, Goldenberg D, Morse S, Whiteley W, Yang R. Graphical properties of easily localizable sensor networks. Wirel Netw. 2009;15:177–191.
    1. Bajaj C. The algebraic degree of geometric optimization problems. Discrete Comput Geom. 1988;3:177–191.

LinkOut - more resources