Extrapolating Metabolic Savings in Running: Implications for Performance Predictions

Abstract

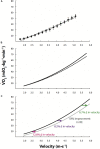
Training, footwear, nutrition, and racing strategies (i.e., drafting) have all been shown to reduce the metabolic cost of distance running (i.e., improve running economy). However, how these improvements in running economy (RE) quantitatively translate into faster running performance is less established. Here, we quantify how metabolic savings translate into faster running performance, considering both the inherent rate of oxygen uptake-velocity relation and the additional cost of overcoming air resistance when running overground. We collate and compare five existing equations for oxygen uptake-velocity relations across wide velocity ranges. Because the oxygen uptake vs. velocity relation is non-linear, for velocities slower than ∼3 m/s, the predicted percent improvement in velocity is slightly greater than the percent improvement in RE. For velocities faster than ∼3 m/s, the predicted percent improvement in velocity is less than the percent improvements in RE. At 5.5 m/s, i.e., world-class marathon pace, the predicted percent improvement in velocity is ∼2/3rds of the percent improvement in RE. For example, at 2:04 marathon pace, a 3% improvement in RE translates to a 1.97% faster velocity or 2:01:36, almost exactly equal to the recently set world record.

Keywords: energetic cost; locomotion; marathon; oxygen uptake; running economy.

FIGURE 1

Oxygen uptake (O₂) increases curvilinearly with running velocity. (A) Linear (solid line) and curvilinear (dashed line) regressions to treadmill running data from 10 high-level male runners (<30-min 10 km) over a wide range of velocities (1.78–5.14 m/s) (Batliner et al., 2018). (B) Batliner et al. (2018) quadratic equation (dashed line) and the quadratic equation combined with Pugh’s cubic term for overcoming air resistance (solid line), as per Eq. [2]. (C) Based on this cubic Eq. [2] (black line), a 10% improvement in running economy (RE; gray line) allows for percent improvements in running velocity which depend on running velocity itself. At slower running velocities (∼<3.0 m/s), O₂ increases gradually with increases in running velocity, and, as a result at 2.5 m/s a 10% improvement in RE should facilitate running 12.6% faster. At faster running velocities, O₂ increases steeply with running velocity and as a result at 5.5 m/s, a 10% improvement in RE should allow for running only 6.7% faster.

FIGURE 2

Predicted percent improvements in running velocity depend on the baseline running velocity. (A) Predicted percent improvements in running velocity vs. running velocity, based on a 4% improvement in RE, using several equations from the recent scientific literature. The solid green is based on a quadratic fit through Batliner et al. (2018) data with Pugh’s cubic air resistance term. The green dashed line is based on a linear fit through Batliner et al. (2018) data combined with Pugh’s cubic air resistance term. The difference between the two green lines highlights the importance of the inherent curvilinearity of the O₂-velocity relation which substantially alters the magnitude of percent improvement in velocity. (B) Predicted percent improvements in running velocity vs. running velocity, based on 1 to 4% improvements in RE, using Eq. [2], which combines the quadratic equation from Batliner et al. (2018) with Pugh’s cubic air resistance term. Beyond the velocity range of Batliner et al. (2018) (>5.14 m/s) prediction lines are dashed.