Response of collagen matrices under pressure and hydraulic resistance in hydrogels

Abstract

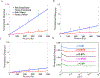
Extracellular matrices in animal tissue are hydrogels mostly made of collagen. In these matrices, collagen fibers are hierarchically assembled and cross-linked to form a porous and elastic material, through which migrating cells can move by either pushing through open matrix pores, or by actively digesting collagen fibers. The influence of matrix mechanical properties on cell behavior is well studied. Less attention has been focused on hydraulic properties of extracellular matrices, and how hydrodynamic flows in these porous hydrogels are influenced by matrix composition and architecture. Here we study the response of collagen hydrogels using rapid changes in the hydraulic pressure within a microfluidic device, and analyze the data using a poroelastic theory. Major poroelastic parameters can be obtained in a single experiment. Results show that depending on the density, porosity, and the degree of geometric confinement, moving micron-sized objects such as cells can experience substantially increased hydraulic resistance (by as much as 106 times) when compared to 2D environments. Therefore, in addition to properties such as mechanical stiffness, the fluidic environment of the cell is also likely to impact cell behavior.

Fig. 1

(A-C) Collagen architecture for different gelation temperatures and levels of cross-linking, imaged using the reflectance mode. (A) 7 mg/ml gelled at 4°C. (B) 7 mg/ml gelled at 37°C. (C) 7 mg/ml gelled at 37°C cross-linked with genipin. The collagen network gelled at 4°C has thicker and longer fibers compared to the collagen gelled at 37°C. 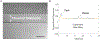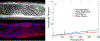The genipin cross-linking does not introduce significant differences in the fiber appearance. Scale Bar = 50 μm. (D) Diagram describing the fabrication of the microfluidic device. After collagen is gelled in the microfluidic channel, a thin rod of diameter 100 μm or 150 μm is pulled from the device, leaving a channel of varying diameter. (E) Experimental setup for changing the hydraulic pressure. Tubes connected to the microchannel are raised and lowered to change the hydrostatic pressure in the channel. (F) Schematics of the channel (created by pulling the Nitinol Rod) filled with PBS with or without MDCK II cells lining in the inner face of the channel. The channel has an inner radius r_i = 50μm and the boundary of the collagen is modeled by an outer radius r_o = 1050μm. Drawn not to scale.

Fig. 2

Response of the collagen matrix to hydraulic pressure changes. (A) A DIC image of the collagen channel 100 μm in diameter. See Fig. 1F for a schematics where 2r_i =100 μm. The diameter of the channel is monitored in time at 10 Hz resolution. (B) Data from pressure change experiment. The channel pressure is increased by five inches of PBS (~1.245 kPa) at t =1 sec, before which the normalized diameter is always 1. The peak (short time response) and plateau (long term response) are obtained from measuring the channel diameter as a function of time. The channel diameter recovers back to the original value after pressure release.

Fig. 3

Spatio-temporal response of collagen matrices of different architecture. (A) Peak and plateau deformations for 100 μm diameter channel with 7 mg/ml matrix gelled at 4°C. Best fitting parameters obtained are: α = 0.97, G = 3.5 kPa, ν = 0.2, ν_u = 0.285, κ = 2.5 × 10⁻¹¹ m², μ ≈ 10⁻³ Pa·s. (B) Peak and plateau deformations for 100 μm channel with 7 mg/ml matrix gelled at 37°C. Best fitting parameters obtained are: α = 0.98, G = 5 kPa, ν = 0.2, ν_u = 0.38, κ = 10⁻¹¹ m². (C) Peak and plateau deformations for 100 μm channel with 7 mg/ml matrix gelled with 1% (w/v) genipin at 37°C. Best fitting parameters obtained are: α = 0.98, G = 6 kPa, ν = 0.2, ν_u = 0.39, κ = 10⁻¹¹ m². The difference between peak and plateau values is significantly larger for matrices gelled at 4°C compared to 37°C and genipin cross-linked collagen. (D) Predicted variations of channel plateau deformation as a function of matrix permeability, κ, and the Biot-coefficient, α. The rest of the parameters are the same as those in panel (A). The pressure change used was five inches of PBD (~1.245 kPa). We observe that beyond certain limit of permeability, the plateau is essentially independent of permeability. All error bars are standard errors.

Fig. 4

Response of a model tubular epithelium in collagen gelled at 37°C. (A) DIC image of a tubular epithelium showing a confluent layer of MDCK II cells in the collagen microchannel. (B) Confocal immunofluorescence images of the confluent MDCK II cells showing F-actin (Phalloidan Red) and nucleus (DAPI, Blue). (C) Peak and plateau deformations of the tubular epithelium of MDCK II cells during hydraulic pressure change. Best fit parameters are: α = 0.94, G = 9 kPa, ν = 0.2, ν_u = 0.4, κ = 5×10⁻¹² m². The channel deformation in the presence of epithelium is significantly smaller than that of the matrix without cells. This suggests that the epithelium resists pressure diffusion and fluid flow into the matrix. The error bars are standard errors.

Fig. 5

Numerical simulations to estimate coefficient of hydraulic resistance, d_g. (A) Schematics of a spherical object moving upwards in axial, z, direction in a 3D poroelastic medium with different levels of confinement. (B, C) Left panels: the velocity of the solid phase from finite element (FE) simulations. Right panels: the fluid pressure field in the matrix pores from simulations. In (B) the radius of the channel is 2,500 μm and in (C) the radius is 40 μm. Both pressure and velocities well decay to zero at the inlets and outlets of the channels. For better visualization, only part of the computational domain is shown (in C, the entire domain is shown). (D) Predicted coefficient of hydraulic resistance, d_g, as a function of κ for different channel confinement. Solid lines: predictions from FE simulations. Dashed line: analytical estimate of an infinite domain given by d_g = μr₀/κ (Eq. 18). Dash-and-dotted line: analytical estimate of maximum confinement d_g = μℓ/κ. (E) Predicted coefficient of hydraulic resistance in the poroelastic medium, d_g, as a function of the radius of the spherical, r₀, for different fluid viscosities in the matrix, μ. Solid lines: predictions from FE simulation. Dashed lines: analytical estimate d_g = μr₀/κ (Eq. 18). (F) Predicted coefficient of hydraulic resistance, d_g, as a function of the shear modulus of the solid, G, for different confinement dimensions. κ = 10⁻¹³ m². (G) Schematics of a spherical object moving in a single phase (Stoke’s flow) with different levels of confinement. (H) Predicted coefficient of hydraulic resistance, d_g, as a function of the radius of the spherical, r₀, for different channel confinement in Stoke’s flow. Solid lines: predictions from FE simulations for Stoke’s flow. Note d_g is significantly lower than in (E) for the same size object. (I) Predicted coefficient of hydraulic resistance, d_g, as a function of the fluid viscosity, μ, for different channel confinement. The solid lines are predictions from FE simulation. and the dashed lines with symbols are from analytical estimates. In (H) and (I), dashed lines with stars are analytical estimates for an infinite domain where d_g = μ/r₀. Circles with or without dashed lines are analytical estimates d_g = 8μℓ/R², calculated from the position of the sphere to the end of the channel. (J–L) Prediction of d_g with a viscoelastic sphere from FE simulations. (J) Predicted d_g as a function of sphere elasticity, E, for different matrix permeability, κ. (K) Predicted d_g as a function of sphere radius, r₀, for different matrix viscosity, μ. (L) Predicted d_g as a function of sphere retardation time, τ, for different sphere Poisson’s ratio, ν_s.