Stochastic coupled map model of subcellular calcium cycling in cardiac cells

Abstract

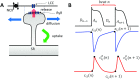
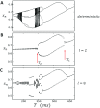
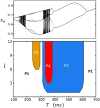
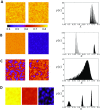
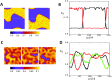
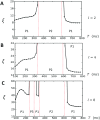
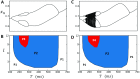
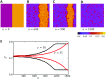
In this study, we analyze a nonlinear map model of intracellular calcium (Ca) and voltage in cardiac cells. In this model, Ca release from the sarcoplasmic reticulum (SR) occurs at spatially distributed dyadic junctions that are diffusively coupled. At these junctions, release occurs with a probability that depends on key variables such as the SR load and the diastolic interval. Using this model, we explore how nonlinearity and stochasticity determine the spatial distribution of Ca release events within a cardiac cell. In particular, we identify a novel synchronization transition, which occurs at rapid pacing rates, in which the global Ca transient transitions from a period 2 response to a period 1 response. In the global period 2 response dyadic junctions fire in unison, on average, on alternate beats, while in the period 1 regime, Ca release at individual dyads is highly irregular. A close examination of the spatial distribution of Ca reveals that in the period 1 regime, the system coarsens into spatially out-of-phase regions with a length scale much smaller than the system size, but larger than the spacing between dyads. We have also explored in detail the coupling to membrane voltage. We study first the case of positive coupling, where a large Ca transient promotes a long action potential duration (APD). Here, the coupling to voltage synchronizes Ca release so that the system exhibits a robust period 2 response that is independent of initial conditions. On the other hand, in the case of negative coupling, where a large Ca transient tends to shorten the APD, we find a multitude of metastable states which consist of complex spatially discordant alternans patterns. Using an analogy to equilibrium statistical mechanics, we show that the spatial patterns observed can be explained by a mapping to the Potts model, with an additional term that accounts for a global coupling of spin states. Using this analogy, we argue that Ca cycling in cardiac cells exhibits complex spatiotemporal patterns that emerge via first or second order phase transitions. These results show that voltage and Ca can interact in order to induce complex subcellular responses, which can potentially lead to heart rhythm disorders.

FIG. 1.

(a) The architecture of Ca signaling in cardiac myocytes. Each dyadic junction contains LCC channels in close proximity to an RyR cluster. Calcium is released into the dyadic junction (dashed rectangle) due to Ca sparks that are initiated by the LCC openings. The released Ca then diffuses into the cell and is pumped back into the SR via uptake pumps. NCX denotes the sodium-calcium exchanger that couples the Ca released to the voltage across the membrane. (b) Illustration of the mapping variables used to describe the beat-to-beat dynamics of voltage and Ca at a single dyad. Top trace shows that the voltage waveform which is characterized by the APD at beat n is denoted as $A_n$, which depends on the previous diastolic interval $D_{n-1}$. Blue trace denotes the SR load at the beginning $[x_{ij}(n)]$ and at the end $[x_{ij}(n+1)]$ of beat n. Red trace denotes the total Ca in the cytosol at the beginning of beat $n[c_{ij}(n)]$, at the peak $c_{ij}^p(n)$, and at the beginning of the next beat $c_{ij}(n+1)$.

FIG. 2.

(a) Bifurcation diagram of the deterministic map. Nonlinear map given by Eqs. (30)–(32) is paced for 1000 beats, and the steady state SR load $x_n$ is plotted for the last 100 beats. (b) Bifurcation of the stochastic map with diffusion coupling set to $l=2$. The $200\times 200$ system is initialized with uniform initial conditions then paced for 1000 beats. The steady state average $x_n$ transitions from an approximate period 1 to a period 2 response beginning at $T_1\approx 600\mathrm{ms}$ then back to period 1 for $T<T_2\approx 350\mathrm{ms}$. (c) Increasing coupling to $l=8$ uncovers higher order periodicities ranging between P1 and P4.

FIG. 3.

The phase diagram of the stochastic map system identifying the boundaries of higher order periodicities of the steady state SR load. The bifurcation of the deterministic map is shown on top for comparison.

FIG. 4.

Spatiotemporal dynamics of the 2D stochastic map at steady state. The system is initialized with uniform initial conditions with $x_{ij}(0)=1$. (a) Coupling strength is set to $l=2$, and the system is paced at $T=650\mathrm{ms}$ corresponding to the P1 case. Snapshots of the system after 1000 beats show that steady state Ca is spatially uniform with small fluctuations. Color bar indicates the local SR load $x_{ij}$. The probability density plotted to the right captures the distribution of $x_{ij}$ at steady state and shows that it is sharply peaked in the range [0.7–0.8]. (b) The system is paced at $T=450\mathrm{ms}$ corresponding to the period 2 regime. The SR load is spatially uniform at steady state with the distribution showing two peaks in the range [0.55–0.60] and near 0.75. (c) At $T=275\mathrm{ms}$, the system exhibits global period 1 behavior as in the case for $T=650\mathrm{ms}$ although the system is spatially disordered. (d) Increasing the spatial coupling to $l=8$ and pacing the system at $T=270\mathrm{ms}$ yield period 3 behavior. The SR load is effectively spatially uniform at each beat and the steady state $x_{ij}$ is distributed around 3 distinct peaks.

FIG. 5.

(a) Starting with random initial conditions, the system can evolve to a steady state heterogeneous pattern. Snapshots of the system show a domain wall that separates two regions that are out-of-phase. (b) 1D cross section of the system along the dashed line shown in (a). Here, the SR load is plotted at beat 1000 (red) and the next beat (black). (c) The system evolves into disordered patterns with regions that are out of phase, when the coupling strength is increased and paced in the period 3 regime. (d) 1D Cross section showing the desynchronized patterns at steady state for beats 1000, 1001, and 1002. Color bars indicate the SR load.

FIG. 6.

The correlation length $\xi$ plotted as a function of T. (a) The case $l=2$ showing that $\xi$ increases to the system size as T approaches the period 2 phase boundary (red dashed lines). (b) Increasing coupling strength to $l=4$ increases the correlation length, with $\xi \sim 23$ for $T<T_2$ and $\xi \sim 14$ for $T>T_1$. (c) When $l=8\xi$ increases near the period 2 and 3 transition. Red dashed lines indicate the period at which the transition occurs between the indicated periodicities.

FIG. 7.

(a) Bifurcation diagram of deterministic system when Ca cycling and voltage are positively coupled. When $\gamma =50$, the period 2 and period 4 regimes are expanded, while higher order periodicities are eliminated. (b). Phase diagram of the stochastic map model showing that the dominant behavior is period 2, while stronger coupling is needed to access the period 4 regime. (c) A larger Hill coefficient $(\nu =50)$ introduces higher order period doubling bifurcations in the deterministic dynamics. (d) Phase diagram of the corresponding stochastic map model showing again the expansion of the P2 phase.

FIG. 8.

(a)–(d) Time evolution of a domain wall that is placed at the center of a $200\times 200$ system. The pacing rate is $T=500\mathrm{ms}$, and $l=3$, so that the system is in the P2 regime shown in Fig. 7(d). The steady state distribution is spatially synchronized and alternates between two SR loads. Color bar indicates the local SR load. (e) The global average SR load $x_n$ as a function of beat number n for two $\gamma$ values. Here, we observe that when $\gamma$ is reduced, the domain walls remain longer in the system.

FIG. 9.

(a) Bifurcation diagram of deterministic system when Ca cycling and voltage are negatively coupled $(\gamma =-55\mathrm{ms})$. The map shows a typical period doubling bifurcation at higher pacing rates. (b) Bifurcation diagram for the stochastic map model with uniform initial conditions $x_{ij}(0)=1$ and spatial coupling $l=2$. To the right are snapshots of three independent simulation runs at $T=400\mathrm{ms}$, showing distinct steady state patterns after 1000 beats. (c) Bifurcation diagram for the case of random initial conditions and spatial coupling $l=2$. Snapshots of three independent runs at $T=520\mathrm{ms}$ also evolve to distinct steady state patterns. Vertical dashed lines indicate the pacing rate at which snapshots are taken.

FIG. 10.

Time evolution of different initial conditions in the case of negative voltage Ca coupling. (a) Evolution of a domain wall that joins two opposite sides of the square lattice. Here, the system is paced at $T=500\mathrm{ms}$ for the beats indicated. (b) Bifurcation diagram of system where the initial condition is the same as that in (a). Bifurcation diagram is shown after 1000 beats. Vertical dashed line indicates the pacing rate at which snapshots in (a) are taken. (c) Evolution of a square domain wall at a pacing rate of $T=500\mathrm{ms}$. The domain walls evolve to form a circular region until reaching a fixed radius. (d) Bifurcation diagram of the system with the initial condition given in (c). Steady state is after 1000 beats. Verical dashed line indicates the pacing rate at which snapshots in (c) are taken.

FIG. 11.

A rectangular lattice with aspect ratio 1:6 initialized with a domain wall along the long axis. The domain walls reorient to join the minimum distance between the two boundaries and divide the system into half. This corresponds to the minimum energy configuration in the case of negative coupling.